Lao Kang
January 25, 2010
ChatGPT translation from 《女儿与斐波纳契数列》
She was ten years old that year, in the fifth grade. The principal recommended her for the “Saturday School” at Milton Academy. She chose the course “Extreme Math.” The homework for the first class asked: Is the 100th term of the Fibonacci sequence an odd or even number?
You might not have heard of the Fibonacci sequence, but you’ve probably heard of methods like the golden ratio, 0.618, or the golden section. Although these have different names, they all originate from the Fibonacci sequence. It’s simple, and you don’t need advanced math to understand it — basic elementary arithmetic and a little patience are enough to grasp the concept:
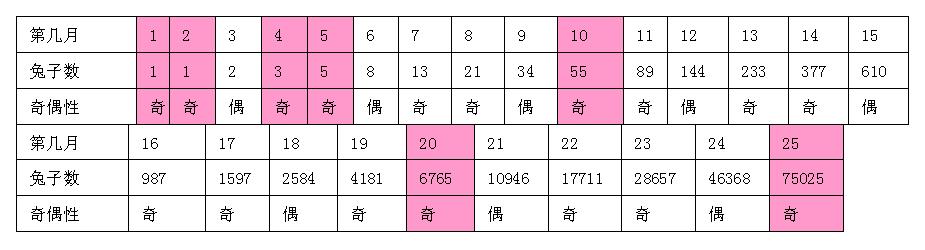
Imagine a species of rabbits that reproduces asexually. They begin reproducing after two months, and thereafter, one baby rabbit is born each month. In the first month, there is only one rabbit, let’s call her Bunny. In the second month, there is still only one rabbit, because Bunny is not old enough to reproduce yet. In the third month, Bunny gives birth to her first daughter, so now there are two rabbits. In the fourth month, Bunny gives birth again, but her daughter is not yet old enough to reproduce, so there are three rabbits. In the fifth month, Bunny gives birth once more, and her first daughter gives birth to Bunny’s first grandchild, making a total of five rabbits. And so on. Each month, the number of rabbits forms a sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, and so on. It’s easy to see that starting from the third term, each term is the sum of the two preceding ones.
It’s not hard to understand. Since these rabbits are immortal, all the rabbits from the previous month are still alive, and each rabbit from two months ago gives birth to a new rabbit this month because they are now old enough to reproduce. So, the number of rabbits this month is always the sum of the rabbits from the two previous months, which is the number of old rabbits plus the number of newborns.
The Fibonacci sequence has many interesting numerical properties. For example, starting from the third term, every second number is a multiple of two, every third number from the fourth term is a multiple of three, and every fifth number from the fifth term is a multiple of five. The most beautiful part is that the ratio of consecutive terms in the sequence approaches the golden ratio of 0.6180339887… The reciprocal of this ratio, the ratio of the later term to the previous one, approaches 1.6180339887…, which is equally fascinating. This perfect harmony showcases the beauty of mathematics and nature! When we renovated our house, we tried to make sure that all rectangular structures or patterns followed this ratio as closely as possible.
The homework in “Extreme Math” listed the first 25 terms of the Fibonacci sequence, and the expectation was for students to observe a pattern: odd, odd, even, odd, odd, even, odd, odd, even… Using this pattern, students could deduce that the 100th term is an odd number.
That day, my daughter stared at the first 25 terms of the Fibonacci sequence, deep in thought. When I got home from work, she excitedly ran to me: “I did it! I did it! The 100th Fibonacci number is odd! I figured it out!”
I quickly looked at her homework and asked, “How did you figure out that the 100th Fibonacci number is odd?”
She pointed to the table she had drawn and said, “The divisors of 100 are 1, 2, 4, 5, 10, 20, 25, and 50. The 1st, 2nd, 4th, 5th, 10th, 20th, and 25th terms in the sequence are all odd. I couldn’t calculate the 50th term because it’s too large, but I think it’s also odd. Since multiplying odd numbers always results in an odd number, the 100th Fibonacci number must be odd.” She proudly explained her reasoning to me.
At that time, my understanding of the Fibonacci sequence was limited to the basic definition that each term is the sum of the two preceding terms and the “odd-odd-even” pattern. This pattern repeats with a period of three. Since 99 is a multiple of three and the third term is even, the 99th term must also be even, so the 100th term must be odd. This was probably the correct method the teacher expected.
So I told her, “Great, your conclusion is correct! But your method might be… well… not quite…”
I hadn’t yet found the right words to explain the correct method without dampening her enthusiasm. She became anxious: “Daddy, I verified it! From 1 to 25, I verified them all! I’m sure I’m right!”
I wasn’t convinced, but seeing how determined she was, I agreed to go through the verification process with her again. The more we checked, the more excited I became—my daughter was indeed correct! Could it be that she had made a significant discovery?
Over the next few days, I was filled with excitement, seeking advice from various people about the validity of my daughter’s discovery. I asked her “Extreme Math” teacher, who responded, “I’ve never heard of that!” My brother-in-law was working on his Ph.D. at the time, and his advisor was very impressed with my daughter’s discovery. He spent several weeks distracted from his doctoral students, nearly jeopardizing my brother-in-law’s dissertation defense.
I calmed down and described my daughter’s discovery in mathematical terms, then tried to prove its correctness. After several attempts, I concluded that, except for the number three, if all the divisors of a number have odd Fibonacci numbers, then that number’s Fibonacci number is also odd. Conversely, if the Fibonacci number of a number is odd, then all its divisors must also have odd Fibonacci numbers.
I was confident in my proof, but I still couldn’t be sure if this was a new discovery or an already known result. It seemed I needed to consult an expert. I wrote a letter to the American Mathematical Society’s Fibonacci Quarterly, explaining my daughter’s discovery process and including my proof. A few weeks later, we received a response from the editor. The letter said that my daughter’s discovery could be considered a corollary of a known theorem. It also praised my daughter for being able to uncover the relationship between the numbers in the sequence and their divisors at such a young age, saying it was remarkable and deserving of recognition. The editor suggested we write an article about my daughter’s discovery and submit it to Mathematics Teacher, a journal for high school math teachers. The letter also included some articles about the Fibonacci sequence, encouraging my daughter to continue exploring and developing in this area.
This happened seven years ago, and thinking back, it still amazes me. First, I’m amazed that my daughter had the focus back then to sit down and work through problems with such determination. Now, her life is much busier: homework, computers, games, chat rooms, friends—she’s busy all day. With the rapid development of the internet, almost any question can be answered online; the days of deep, contemplative thinking are long gone. Second, I’m glad that I didn’t hastily dismiss her discovery at the time. Instead, I put in the effort to confirm its correctness. I also had a lot of fun and learned a great deal. But how much impact will this small episode have on her life?
College applications only consider achievements from high school, so this “feat” was overlooked because my daughter was too young at the time, much to my disappointment.
April 2009, Newton, Massachusetts, USA
All rights reserved by the author.