华新民先生的“爱因斯坦错了,但错得富有成果”等三篇文章(华新民 2023a, 2023b, 2023c),用非技术性的日常语言,简介了近代物理学革命性的突破。这样的工作很有意义。我有一种看法:一个人无论受教育多还是少,学什么学科,从事什么职业,有什么样的兴趣,对现代科学,尤其是物理学和生物学在二十世纪的发展,都应当有所了解。因为这两门学科的发展,严重地冲击了长期被当成是科学世界观的机械论,使得人类的思维方式、宇宙图景起了翻天覆地的变化。缺乏这些方面知识,就难免对在现代科学冲击之下形成的新观点、新思维茫然不解、抱残守缺、固步自封, 甚至盲目自大,不加思考就不由分说地反对。
但要达到这样一种理想的目标,困难也显而易见。姑且放下兴趣问题不说——有相当多的人,对科学兴趣缺缺,满足于中学教育的科学内容,认为那些已经足够应付日常需要,足够作为支撑自己世界观的基础了——,仅仅是技术上的问题,就会难倒大部分科学家。因为,用非技术的日常语言叙述一门学科,要能够把握学科的哪些内容是公众最需要了解、而且能够理解的, 要在专业的精确性和公众的可理解性之间,保持一种适当的平衡。想做到这些谈何容易!
即使困难众所周知,近代以来的大科学家们,如爱因斯坦(Albert Einstein),海森堡(Weiner Heisenberg),维格纳(Eugene Wigner),费曼(Richard Feynman),温伯格(Steven Weinberg),霍金(Stephen Hawking),一直到还健在的彭罗斯(Roger Penrose),赛林杰(Anton Zeilinger)——他们的名字如雷贯耳,除霍金之外都是诺贝尔物理学奖获奖人——,在他们终身追求物理学突破的繁忙生涯中,没有放弃科普事业。他们或是做讲座,或是写书,将本学科的新进展用外行听得懂、读得懂的语言介绍给公众。因为他们知道,科学的突破,尤其是那些冲击人们世界观的科学突破,只有在为公众理解的情况下,才能发挥出最大的功效,才能起到最好的社会效果。我自己对马克思主义的理论基础从相信到怀疑、最终决裂,就起始于十九岁那年阅读爱因斯坦的一部介绍相对论的普及读物。这一经历,将来有机会向大家介绍。而且,世界上有谁不需要科学普及读物?即使是爱因斯坦,在物理学之外,也需要普及性读物来得到非本行专业的知识。总不能指望他能够读懂1953年沃森(James Watson)和克里克(Francis Crick)提出DNA双螺旋结构的论文、或者认为他不必了解现代生物学上最重要的发现吧?
科普最大的障碍,是科学知识的数学表达。俗话说,“多一条数学公式,就少一半读者”。
在很长一段时间内,我就想把现代数学-科学两条重要的定理介绍给读者。 一条是“哥德尔不完备定理”,在踌躇多年之后,写了一篇“哥德尔和他的两条不完备定理”。另一条就是华先生文章提到的以“贝尔不等式”(Bell’s Inequality )为基础的“贝尔定理”(Bell’s Theorem)(注1)。和哥德尔不完备定理不同,作为贝尔定理基础的贝尔不等式其实非常简单,有中学数学知识已经足够;贝尔不等式在数学上也没有创造,不像哥德尔为证明其定理首先创造了一套“哥德尔编码”(Gödel’s Encoding)。
作者就班门弄斧一回,以贝尔(John Bell)、巴古特(Jim Baggott), 罗森柏鲁姆(Bruce Rosenblum)和库特纳(Fred Kuttner),赛林杰等人的解说为基础,把这条不等式介绍给读者。首先介绍贝尔不等式的数学表达——这非常简单,只要跟着一步步推理,可以担保读者一定理解;然后介绍这条不等式和量子力学的关系。这两部分,作者毫无创造,完全是综合、转述物理学家们的解释。最后讨论贝尔定理的意义。在这方面,作者也仅仅是把科学界就贝尔定理提出的最重要的两个问题概括一下,以便读者思考。
贝尔不等式的数学表达
概括一下,贝尔不等式
1. 涉及成对的物体的三个量,这里用a, b, c表达。成对的物体,比如一对对光子, 一双双手套等。
2. 运用了概率统计。
3. 结果是,在日常生活中,如果这条不等式不成立,那么就是一个无法理解的荒诞世界。
我们用一双手套做例子。一双手套,使用的材料、制造工艺、颜色……等等完全一样。唯一不同的是一只“左向”,戴在左手上;一只“右向”,戴在右手上。这两只手套之间具有100%的相关性。这里需要注意,“相关性”(correlation)不能理解为“等同性”(identity)。两个物体相关,有可能某种性质完全等同,也可能完全相反。“相关”指的是两者之间具有某种不变的关系。比如一双手套拿出其中的一只,发现是左向,可以肯定另一只一定是右向。请记住,这些是既定的、和任何实验无关的相关性。
我们用一些手套来做三次实验:假设手套的材料比较差, 用洗衣机经过一定温度的水洗,有些就会损坏。这三次实验可以如下设计:
实验a. 用0度的水洗1小时;
实验b. 用22.5度的水洗1小时;
实验c. 用45度的水洗1小时。
洗过了未损坏,我们标记为+, 损坏了就标记为-。三次实验,每次实验有+-两种可能的值,2的3次方为8,即有8种可能:
我们用下面的方法来表达实验的结果:n(a+b-),括号中的字母表示做的是什么实验,这里表示是上表的实验a, 实验b;+号表示实验通过,-表示实验未通过(这里就是手套损坏了),n表示数量。这个表达的意思是“手套做实验a通过,实验b失败的数量”。依次类推, n(a+b-c+)表示通过了a, c的实验,实验b 失败了, 等等。
现在,我们用水洗一些手套——注意,暂时我们还不考虑成双的手套实验——,统计一下结果。下面的结果一定成立:
(1) n(a+b-) = n(a+b-c+) + n(a+b-c-) 表示“实验a通过,实验b未通过的手套的数量,等于实验a通过,实验b未通过,实验c通过的数量,加实验a通过,实验b未通过,实验c未通过的数量之和。”这条公式的可靠性显而易见。观察一下等式的右边就可以发现,实验c通过或不通过,结果都是实验a通过而实验b失败,因此实验c的结果不影响公式的值,可以去掉。去掉c,就是左边的项。以下的公式不再用自然语言解释。
(2) n(b+c-) = n(a+b+c-) + n(a-b+c-)
然后把(1), (2)相加(等式两边各自相加),得
(3) n(a+b-) + n(b+c-) = n(a+b-c+) + n(a+b-c-) + n(a+b+c-) + n(a-b+c-)
为方便起见,我们可以重新安排一下等式右边各项的次序, 得
(4) n(a+b-) + n(b+c-) = n(a+b+c-) + n(a+b-c-) + n(a+b-c+) + n(a-b+c-)
观察一下(4)的右边,第1,2 项中的a只能是+,c只能是-,但b却可+可-。因此不管b是+还是-,与整个公式的值无关,可以去掉b而将两项并为1项, 得n(a+c-),并以此替换(4)中的n(a+b-c-) + n(a+b+ c-),有
(5) n(a+b-) + n(b+c-) = n(a+c-) + n(a+b-c+) + n(a-b+c-)
这里稍微要动一下脑筋:等式右边的n(a+b-c+) + n(a-b+c-)绝不可能是负数,因为这些实验结果相加,n最少也是0,不会出现如“-3只手套没有通过实验c”这种不合理的情况。我们从等式右边去掉这两项。等式右边去掉两个等于或大于0的项,结果左边至少等于,也可能大于右边,下面的不等式一定成立:
(6) n(a+b-) + n(b+c-) ≥ n(a+c-)
这已经近于贝尔不等式了。但仔细想一下,就会发现不严密之处。比如说,如果一只手套没有通过实验a就损坏了,无法再进行后续实验;即使通过了,水洗过程已经对手套的质量有所改变,再用来做另一种实验,结果不精确。因此需要精确化一下,规定:用完全一样的三批成双的手套,左向/右向一双双配好,来做三种实验, 每批成双的手套分别做a,b,b,c、和a,c实验,三种实验各自所用的手套的数量一致,每双手套只做一次实验。
现在我们用一双双手套来做实验:左向的来做实验a, 右向的做实验b,实验a通过,实验b失败的数量记作
(7) N+-(a, b)
请思考一下,如果一双手套两只实验结果互不相关,一双双手套的实验结果当然和一只只手套的实验结果一样,因此有
(8) N+-(a, b) = n(a+b-)
同样有下面的替换
(9) N+-(b, c) = n(b+c-); N+-(a, c)= n(a+c-)。
以N+-(a, b),N+-(b, c), N+-(a, c)替换(6)中的n(a+ b-),n(b+ c-),n(a+ c-), 不等式的值不变,得
(10) N+-(a, b) + N+-(b, c) ≥ N+-(a, c)。
然后,把这个公式中的每一个数量N,除以实验手套的数量,得到实验结果的概率P:
(11) P+-(a, b) + P+-(b, c) ≥ P+-(a, c) (Baggott 2004,p.335-336)。
用自然语言重述一遍,就是“左手套在水温0度下通过水洗,而右手套在水温22.5度下被摧毁的概率, 加上左手套在22.5度下通过水洗,右手套在45度水温下被摧毁的概率,大于等于左手套在0度水温下通过水洗、而右手套在45度水温下被摧毁的概率。”仅仅凭直觉,就能够懂得(11)应当成立!
这就是贝尔不等式,以这条不等式为基础的“贝尔定理”被称为 “最为神秘和深刻的定理” (曹天元 2020, p.209),甚至被称为是“哥白尼以来物理学影响最深远的发现”(Zeilinger 2010,p.273)。
如果跟随上面的推理一步步推导, (11)都是天经地义成立的,如果不成立,我们岂不是生活在一个荒诞的世界?! 我们可以想象一只苹果大于等于一只西瓜,一只一只猪大于等于一头象,但我们无法想象 25+25 ≥ 75!就如在哥德尔不完备定理的证明中,无法接受逻辑推演出“A并且非A”这样的命题(注2)。
难理解吗?只要有中学数学知识,都不难。 所谓“难”其实是有些人不愿意做一步步推导的这样的死工夫。这一段,是Baggott(2004, p.154-157, p.335-336)等文献的译述。作者只是把原来用来做例子的每双袜子总是一只粉红,一只非粉红换成了比较自然的一双手套,一只左向,一只右向。而且考虑到读者的高教育水准,省略了那些不必要的、“替读者思维”式的叙述而已。
需要指出,到这里为止我们讨论的纯粹是数学问题,丝毫没有涉及物理或者哲学。如果用像d’Espagnat(1979), Baggott(2004)等用集合论上的文氏图(Venn diagram)来表示公式(11)及其推导过程,会直观很多,一眼就可以看出(11)左边的两项之和起码等于右边的一项。考虑到并非所有读者都熟悉集合论的表达方式,最后作者放弃了用文氏图的构想。
为什么贝尔不等式与EPR有关?
华先生的文章介绍了EPR的思想。上文的(11), 是一个数学上的不等式。这个不等式怎样和EPR有了关系?以下是作者简要的介绍。
首先必须强调,下面的叙述采用了Bell(1997)策略,没有引入不为公众熟悉的物理量,比如“自旋”(spin), “跃迁”(jump) ,角动量守恒(Conservation of angular momentum)等等。虽然这些物理量和量子的行为及EPR实验密切相关,为简化叙述,便于理解,都省略了。甚至也没有提及有争议的“观察”的作用。这相当于把一份解释工程的草图画成了一幅示意图。有关这些物理量的意义以及它们和EPR实验的关系,请看华新民(2023a)的说明。因此以下解说只能用来从原则上理解贝尔不等式和量子力学的关系,不能用来理解量子的物理特征和实际行为。这一点请务必不要忽视。
现在我们将一双手套换成一对光子,我们以光子偏振(polarization)实验来代替手套的水洗实验。
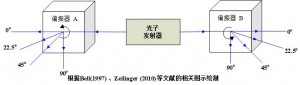
设有一个光子发射器,向其两侧,水平相反的方向发射一对对光子。光子以光速向左右两边移动。根据相对论,光速不可超越,因此一旦发射出去,两光子间不可能再有信息传递。这里光子相当于手套。
在光子移动的水平路径上,左右两边各有一个偏振器(polarizer),能够把光子偏振一个角度。这个偏振器相当于水洗手套的洗衣机。
水温,相当于光子被偏振器所偏转的垂直角度:水温0度相当于垂直角度为0,水温 22.5度相当于垂直角度为22.5度,水温45度相当于垂直45度。请看下面的示意图:
假设我们向一个偏振器发射一个光子,如果偏振器将光子偏转的垂直角度为0度,由于光子自身的特性,这个光子通过偏振器并且在水平方向被探测到的概率是100%;如果偏转的垂直角度是90度,那么光子被偏转到垂直方向被吸收,水平方向被探测到的概率是0。
然而,光子被偏转的垂直角度为45度、22.5度呢?这个光子无法一分为二,一部分走向垂直方向被吸收,一部分走向水平方向被探测到。这时只能统计光子被探测到和被吸收的概率。实验就是要看看,经过偏振器之后,水平方向被探测到和垂直方向被吸收的光子的概率(Zeilinger 2010, p.75-79), 相当于经水洗后未损坏和损坏的手套的概率。请注意,这仅仅是比喻,是粗略的概述,实际情况要比这里说的复杂很多(注3)。
把水洗手套实验换成光子实验,就是
P+-(a, b) ,一对光子向两侧水平移动,左边的光子通过偏振器后仍然水平;右侧则被偏转22.5度,最后统计左边被探测到了、右边被吸收了的概率。
P+-(b, c)表示,一对光子向两侧水平移动,左边的光子被偏振器垂直偏转角度为25.5度;右侧则偏转45度。两边的光子被偏转了不同的角度,最后左边被探测到了、右边被吸收了的概率。
P+-(a, c) 表示,一对光子向两侧水平移动,左边的光子被偏转的垂直角度为0度,仍然水平;右侧则偏转45度,最后左边被探测到了、右边被吸收了的概率。
这样,光子实验和上文水洗手套的实验就对应了,也容易理解了。 这里的叙述,概括了Bell(1997), Baggott(2004), Zeilinger(2010),Rosenblum et al(2011)等文献的相关叙述。
量子物理学界早就有计算(11)中每个项概率的方法:如果一对光子实验的结果是++或者–, 以P++(a, b)为例,其计算公式是1/2 cos^2 (b-a),这里“b-a”表示b的偏振角度减去a的偏振角度;如果是+-或者-+,一个通过而另一个被吸收,则是1/2 sin^2(b-a)。这是简单的三角函数计算,大家都会。因此,可以预期有下面的结果:
实验1:1/2 sin^2(b-a) = 0.073 22.5度减0度等于22.5度。概率为22.5度正弦平方的一半。
实验2:1/2 sin^2(c-b) = 0.073 45度减22.5度等于22.5度。概率为22.5度正弦平方的一半。
实验3:1/2 sin^2(c-a) = 0.250 45度减0度等于45度。概率为45度正弦平方的一半。
把实验预期的结果带入(11), 得到
(12) 0.073+0.073 ≥ 0.250
根据量子物理学家的计算,贝尔不等式(11)不成立!请问,您能够接受这样的结果吗?按照贝尔一开始的计划,实验结果不应当出现(12),不等式(11)应当成立,因此量子力学的理论不完整,一定存在着某种“隐参量”(hidden variable),我们还不知道的参量,使得(11)成立,不会出现诸如(12)这种荒谬的结果。爱因斯坦不知道有贝尔不等式。根据他的思想,(12)是无法接受的,因此一定存在隐参量。
然而,从法国Alain Aspect小组1982年的首次实验以来,所有的实验结果,都证明了确实(11)不成立!这些,华先生的文章已经说清楚了,此处不再重复。
贝尔不等式实验的结果说明了什么?
到现在为止,本文已经用了12条数学公式,当然是非常简单的初等数学公式。那些用到数学分析的内容,即使非常简单,也丝毫未提及。然而,用本文开始所引用的“一条数学公式将减少一半读者”的规律,(1/2)^12,理论上读到这里的读者只剩下一开始的0.0244%!
当然不会如此,毕竟CND有一个高教育水平的读者群,所用的公式大家都懂。下面没有数学了,希望读者数量能以每段翻番的数量增加!然而,这又不得不涉及有些人不屑一顾、误认为可以任意狂想、毫无根据乱说的哲学!为了避开纠缠到这一误解中去,这里不引用任何哲学家的论述而只是重述物理学家的提出的问题。
第一个问题是,为什么说贝尔不等式在实验中不成立,说明不存在隐参量?这里用一个比喻来说明。
我们把这里的一对对光子换成一对对双生子,他们每一对生物基因完全一致,其中一个我们称为a, 一个称为b。他们的皮肤、头发、眼睛的颜色完全一致。
后来这对双生子分开了,其中一个感觉头发颜色不好看,就染成了其他颜色。另一个的头发颜色是不是会跟着也变了颜色?
人人都会正确地回答:不会。为什么?因为双生子头发颜色是基因决定的,不是其中一个后天获得的颜色决定的。
您这就掌握了贝尔不等式的关键之处:这里基因就是决定头发颜色的隐参量!但是,假如一对双生子原来的头发是黑色,其中一个a感觉黑色不好看,染成了金色——现实生活中这种经常事情发生——,而b的头发也相应地变成了金色或者别的什么颜色,那说明什么?说明基因,也就是隐参量没有起作用,而是双生子中一个的行为起了作用!这个例子,是Bell(1997)采用的。
再来看看光子实验,正是因为一对光子之一实验的结果和另一个光子的实验结果相关, 而不是和它们事前确定的特征相关,两个光子之间的状态具有“动态”相关性(注4),就是近年大家熟知的所谓“纠缠”(entanglement),(11)才不成立!我们为什么要假设存在一个不会起任何作用、也从未被观察到的参量?贝尔定理告诉我们,隐参量不存在! 这就相当于说,生物学上没有基因这回事。(Bell 1997)
贝尔不等式实验的第一个意义就是:隐参量不存在,局域实在性(local realism)不存在。本文也不引入局域性的形式定义,而使用自然语言来粗略地说明:有两个事件A, B发生, 如果根据物理定律两个事件之间不可能发生信息交换的话,那么事件A的行为与事件B的行为互不影响。
这就是贝尔定理的内容: 局域性与量子力学不相容。
上文的光子实验中,光子以光速向相反的方向移动,其速度是光速。信息交换不可能超过光速,但一对光子中的一个测量的结果却和另一个光子的测量结果相关。“局域实在性”被打破。这是多数物理学家都能接受的定理。
有些物理学家则进了一步,提出了下面的问题:是否存在一个独立于观察存在的实在?这就是“实在性”(realism)问题。
我估计读者中的99.9%会不假思索地回答,当然。毫无疑问存在一个独立存在的客观世界,人类观察与否它都存在。人类不观察月亮,月亮就不存在了吗?这不仅是我们从小受到的科学、哲学教育所说的,而且和我们的直观,和我们从某些不言自明的前提出发的逻辑推理的结论相符合。
我无意去改变任何人的信念,只是认为,这不是一个不需要考察、思考的命题。也许经过考察、思考之后结论不变。但不经过考察、思考,根据过去的教育和直觉,就认为这个命题天经地义地正确,那和迷信有什么差别?
对“存在独立于观察的实在”能够提出问题吗?当然!
比如说,人类目前、甚至永远无法观察到、更不用说证实的超弦(super string)、圈引力(loop gravity)、暗物质、暗能量是不是实在?也就是很多人说的“客观存在”?这些是人类根据可观察、可证实的现象假设、推理的结果。如果承认它们是实在,那么谁能保证将来的科学不会推翻这些概念?总不能说我们承认他们是“暂时性的”的实在吧?古人不也曾经假设过有一种“燃素”(phlogiston)作为燃烧的基础吗?直到19世纪末,科学界不是还假设存在“以太”(ether)吗?总不能说“燃素”,“以太”在古时候是实在,当代不是了吧?
好,我们现在排除掉一切如超弦之类的推理、假设,只承认那些被观察到的、可证实的部分为实在,那么总可以了吧?
可惜的是,这又导致下面一个命题:您见过没有被(直接或间接)观察到的实在了吗?排除了超弦之类,回答只能是没有!然而,下面这个命题您怎么看?
“实在是必须被我们观察到的、却又不依赖我们观察的存在物”,这个命题有没有矛盾?(Baggott, 2004, p.118)
因此,我们陷入两难:要不承认存在无法被观察到的实在,要不承认实在和观察不可分。
还有,如果我们不承认那些不能被观察到的存在是实在,等于说宇宙间的一大部分,人类还只是推测,没有知识——这当然是对人类知识状态的唯一合理的陈述——,那么,从有限知识通过不完全归纳得出的命题“实在必须是被我们(直接或间接)观察到的存在”,我们用什么来保证它的可靠性?靠直觉还是靠信念?
吴西风“物理是对真实世界的描述吗?” 一文,对这个问题有准确的概括。文中的下面两点实际上就是“实在性”问题:
“(7) 真实世界的存在与否是个悬而未决的问题,无法排除我们所感知的和测量的,其实是个精心设计的模拟程序的运行结果。‘真实的世界’可能并不存在,只是我们的感知所造成的幻觉。
(8)我们的感知影响着实验观测,也就是说,实验观测既是客观的,也是主观的,我们难以分清客观和主观对于测量结果的影响程度。” (吴西风 2021)
这里概括的是物理学界、哲学界争议极大的两个问题,短期内学术界或公众不会形成共识。
事实上,作者本人也不知道答案。对一个问题的答案,除了“是”和“否”之外,还有“不知道”。丁肇中教授对物理学问题,经常会说“不知道”。 2014年在中国的一次讲座上,面对听众的提出的物理学问题,曾经“十问十不知”,而且说过自己的“不知道”使得他获得信任。作者本人只能回答,对实在性问题,不能假装知道,自以为知道,不许别人不知道。作者不同意的仅仅在下面这一点:
“存在一个独立于观察的实在”是一个不需要思考、不需要讨论的不言自明的命题。
即使坚持“存在一个独立于观察的实在”的爱因斯坦也曾经说过,
“对物理学来说非常基本的一点就是,我们假设存在一个独立于我们任何感官行为的真实世界——然而,对此我们不知道。”(Rosenblum 2011, p.166)爱因斯坦自己将“知道”用斜体字加以强调。他只是认为,那个命题是假设,是信念而不是知识,是“不知道”但相信如此。
虽然“存在一个独立于观察的实在”曾经是被认为是不容置疑的、已经成为经典学说的一种观点。但“从来如此,便对吗?” 我们就不需要对已经成为某种传统的学说重加考察?当然不是!科学的每一次突破,都隐含对某种传统的超越。事实上,贝尔本人就曾说过,“人一生的某个时段,总得学一些新的传统。”(Bell, 1997)
最后,Bell指出,Locality 蕴含Determinism (“局域性”蕴含“决定论”,Bell 1997)。这个问题很重大,作者曾在“百年苍黄溯源头——五四新文化运动再批判”系列文章中简要提及过,在此一言难尽,将另文讨论。
余论
这回作者又“跨界”,因而也是“犯忌”地做了一番明知不能为而为之的工作。这么做是出自于作者本人的一个经验:任何科学理论,只有懂得它的数学表达之后,才能真正体验到它的力量。 作者综合了几种文献,还不得不作了简化,只叙述文献中与贝尔不等式相关的部分,去掉了有关光子特性、行为的部分,去除掉无关议论和那些“代替读者思考”的论述。那些都不是专业文献,而是面向非专业人士的讲座或读物。如果说专业文献等于是工程上的设计、施工图纸,普及性文献如同简图,作者的解释就只是示意图。因此,完全谈不上精确。尤其是比喻的部分,任何人都可以在光子和手套、双生子之间找出无数的不可比处;任何一个物理专业的大学一年级学生都可以指责我忽略掉了量子的很多重要性质。但作者相信,为了使公众理解一条涉及很多专业物理概念的公式,遵循贝尔等人的策略,以比喻、简化来叙述,是唯一可能的途径。早在三十多年前,我就曾经提出,做普及性工作,“宁欠精确,必须可理解”。因为读者理解了,可以进一步读更精确、更专业化的文献,不理解则断绝了所有的可能性。
这就是常说的“嚼饭哺人”的工作。所“嚼”的即使是美食,这一“嚼”也就使得风味大减,被“哺”的当然也就更感觉加无滋无味。但如果能使读者有兴趣去尝尝几位作者原来的烹调, 去看一看那些简图、甚至设计图、施工图,那作者的意愿也就得到了充分的满足。
当然,如果作者的示意图歪曲了简图,作者负全部责任。
2023年八月
参考文献
Baggott,Jim(2004), Beyond Measure: Modern Physics, Philosophy, and the Meaning of Quantum theory.
Oxford University Press, Oxford, UK.
Bell, John (1987), Speakable and unspeakable in Quantum Mechanics.
Cambridge University Press, Cambridge, UK.
(1997), “Indeterminism and nonlocality”. In Driessen et al(1997), p. 83-100.
曹天元(2020), 《量子物理史话:上帝掷骰子吗?》。八方出版股份有限公司,台北,台湾。
d’Expagnat, Bernard (1979), “The Quantum Theory and Reality”. In Scientific American, Nov., 1979,
p.158-181
Driessen, A. and N. Suarez(1997), Mathematical Undecidability, Quantum Nonlocality and the Question of
the Existence of God. Springer Scienced + Business Media Dordrecht, B.V., Germany.
华新民(2023a), “爱因斯坦错了,但错得富有成果”。载《华夏文摘》06/13/2023
(2023b), “玻尔没有错,但挨了几十年批判”。载《华夏文摘》06/14/2023
(2023c), “马赫不承认微观粒子的存在,却影响了一代量子物理学家”。 载《华夏文摘》06/15/2023.
Rosenblum, Bruce; Fred Kuttner (2011), Quantum Enigma: Physics Encounters Consciousness. Oxford
University Press, Oxford, UK.
吴道平(2019), “百年苍黄溯源头——五四新文化运动再批判(八) 新文化运动的科学观批判”。载《华夏新文库.吴道平文集》。
吴西风(2021), “ 物理是对真实世界的描述吗?”。 载《华夏新文库.吴西风文集》,02/20/2021.
Zeilinger,Anton(2010), Dance of the Photos: From Einstein to Quantum Teleportation.
Farrar, Straus and Giroux, New York, NY, USA.
注释:
1. 作者没有找到贝尔定理的形式表达。 贝尔自己的说法是“…if is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local.”(Bell, 1987, p.65),即局域性与量子力学不相容。贝尔表述的意义将在下文讨论。
2. 有个朋友在读完我的“哥德尔和他的两条不完备定理”之后,和我通讯,说将来科学的发展必定能够推翻哥德尔不完备定理,解决形式系统的完备性问题。这就是把逻辑矛盾和因知识限制造成的无知混为一谈了。不管将来科学发展到什么地步,“A并且非A”不可能成为正确命题。
3. 例如,我们不应当笼统地说光子走了某一条路径。在被实际被探测、纪录之前,光子是处于叠加态。了解光子双缝实验的读者都了解,单个光子同时走过了两条路径。最终的位置在被观察到的时候才能确定。 说光子“被吸收”也是Zeilinger(2010)采用的一种简单化的说法。
4. 关于动态相关,华新民(2023a)解释如下:“两个处于纠缠态的粒子遵守实在性和局域性的要求,也就是说,它们如同一双鞋子或一副手套那样,自始至终保持着人们常识所理解的那种一左一右状态,与是否测量无关,那么它们的相关性就是事先确定的,