–兼谈以色列与哈马斯战争对台湾防御的经验教训
摘要 – 台海问题毫无疑问是世界地缘政治、军事、经济最重大的问题,是民主和威权专制对决的关键。如不理性控制而引起世界大战,不仅会导致重大伤亡,而且会立即导致世界经济大衰退【1,2】。智慧通导台海问题,需优化短期和长期战略。本文主要目的是论证短期战略,以维护和平减少战争风险。为此,我们用数学和经济学博弈论来分析冲突各方的潜在益损,并力求数据的准确和客观性,消除武断和偏见,客观论证维持和平是对各方最有益的理性政策。台海的主动权主要在中共,而台湾、美日等西方阵营为另外一方或多方。冲突的决策树则根据各方的益损而顺序展开。传统博弈论给博弈各方赋予单个益损值以便于计算,所以忽略很多重要的信息。本文用矢量来表达各方的益损变量,以改进传统方法的缺陷,实现决策里常见的多目标诉求。此举优点突出,它可以不必估算各个目标分量的详细数值,只需进行矢量的帕雷图(Pareto)优化意义上的益损比较,就能找出一个矢量对另一个矢量的相对优势,最终得出帕雷图-纳什(Nash)均衡。益损矢量和Pareto方法是一个强大的分析工具,它可以比较各个策略里主权、尊严、军事经济益损等不同质目标分量,而不局限于传统方法里只比较单个同质指标。在只有大陆和台湾二者参与的博弈里,台湾的未来主权地位难以维持;但是在美国为首的民主阵营参与下,台海的Pareto-Nash均衡就是维持和平。本文还初步总结了以哈战争的经验教训,特别是哈马斯如何在强大的以色列军事力量防御和进攻下,能用灵活机动的分布式力量、地道系统、和国际舆论坚持数月而避免被歼灭,很值得弱势方借鉴。博弈论是个宏大的题目,为了叙述清晰且避免篇幅过长,本文以前后篇展出,前篇主要分析如果只有大陆和台湾参与军事博弈情况下,什么是博弈均衡解,后篇则分析加入美国为首的西方阵营后的博弈均衡解, 以及可能的多赢策略。
1. 前言
兰德研究员一个新异的观点是,美中二国都已衰退且国内问题成堆,二者已是在进行新中世纪世界类的竞争,所以难以进行大规模战争【3】。但是不同的声音大量存在,美国众议员M. Gallagher就在华尔街日报刊文说不能指望中国因经济问题而放弃攻打台湾,俄罗斯经济不好,但是从2014年以来普京亦然不断入侵乌克兰【4】。美国新任印太司令帕帕诺今年二月在参议院作证,说中共随时可能攻打台湾【5】。CIA也于去年在参议院作证确认,习近平已经指示PLA做好随时攻打台湾的准备【6】。本文主要用Pareto-Nash博弈的概念来研究台海冲突的博弈均衡,并把经典博弈益损表里的单个数值替换为包含多个分量的矢量,以反应现实世界博弈里不同质目标的优化。结果表明,这个新模型是对传统博弈论很好的改进。本文还把决策树和博弈论结合在一起,以使得讨论更直观和清晰。所以,我在下面先简介博弈论。
常言人生如戏,戏演完了,就该向苏轼那样感叹人生如梦了。真正能概括事物的警句莫过于“世事如棋”,楚河汉界,变幻莫测【7】。人生就是广义的赌博,选择配偶就是重大赌博,所以苏格拉底说“还是娶老婆吧,娶了个好的你就爽歪了;娶了个坏的你就成了哲学家!”【8】 人生如此,国家亦然,法国二战时赌希特勒会正面进攻马其诺防线和北部防线,结果希特勒偷袭二者之间薄弱的阿登地区,导致法英联军在敦克尔克大败而逃,不仅亡了国还让德国士兵霸占了大量法国漂亮女人(战后在法国的德兵后裔倍受歧视)【9】。与赌博相关的更带学术性的,是被称为博弈论的谋略研究。博弈是人类和动物社会活动最普遍的现象,所以引起了高知大咖们的青睐。大家小时候就知道田忌赛马的故事,是讲战国时代无腿将军孙膑如何调度上中下三马出场的顺序,以下马对对方的上马、上马对其中马、下马对其上马,实现了三赛二胜,从而帮田忌赢得与齐威王的赌马比赛。
现代博弈论的发展很具传奇色彩。它最早由法国数学家Cournot于1830年代提出,是其观察当时矿泉水双头垄断用供给量来做竞争手段时, 产生了灵感后发明的数学模型【10】。 市场双头垄断公司共用同一个消费函数,市场价格总是位于消费函数上的某一点。二者都根据自己了解的对方的销售量来决定自己的销量以使利润最大化,由此可以得出Cournot博弈均衡。他活着的时候其理论老被经济学界挑刺排挤,没想到死后却声名鹊起,成了主流经济学的经典。与Cournot博弈不同的另一个模型是领头-跟随博弈,由德国纳粹经济学家Stackleberg于1930年代初发明【11】。该模型也是为双头垄断情况发明的,不同的是,它预设市场有个领头者,先根据自己的情况用销量来预置市场价格,另一个则扮演跟随者的角色,根据市场价格来确定利润最大化的销量。该模型准确描述很多现实博弈,如美国司法部2023年起诉亚马逊公司,就是因其采用类似的博弈策略,先把某商品提价,用算法追踪其它零售商看看它们跟随提价还是不跟随。如果有足够多的零售商跟随,亚马逊就保持这个价格【12】。从1920年代末开始, 匈裔美国数学家John von Neumann对博弈论做了大量研究,与以前的研究相比,他把博弈从连续变量扩展到离散变量领域,其中包括著名的零和博弈(Zero-sum game),开启了混合博弈策略的时代【13】。在1944年,他和德裔美国经济学家Oskar Morgenstern出版了一本“博弈论和经济行为”的经典专著 【14】。 当然,谈论博弈论,绝对少不了纳什(John Nash), 一个不幸得了精神分裂症的普林斯顿的数学天才。2001年美国出了一部著名电影《美丽心境》,讲述他如何在1950年代年青时发明了著名的纳什博弈均衡论,同时又幻想自己帮助国防部做破解苏联密码的挣扎,如何在爱妻帮助下与病魔搏斗逐步回归正常人的生活,并于1994年获得诺贝尔经济学大奖。我那时正在研究博弈论在能源系统里的应用,所以看了二遍《美丽的心境》,并深受感动。 Nash博弈均衡概括了前人成果,把理论扩展到多人博弈,包括离散和连续变量的博弈【15-17】。博弈论现在不仅广泛应用于经济学,也用于控制论、计算机、军事、政治学、国际关系等等领域【18-24】。
Nash均衡论有个著名的囚徒困局,讲二个共犯被抓捕后关进二个不同的囚室。由于无法串谋,每个囚徒都得权衡共犯的态度来决定自己招不招认。如果二个都不招,警察在没有其它证据的情况下就不得不释放他们,于是二人都获得自由,收益各为正数1点。如果一个招认一个否认,招认者获得奖励二个点,否认者惩罚一个点为-1。如果二个都招认,则二个都判刑,收益为0。这个博弈可以用表1来表示, 其中括弧里的第一个数值代表囚徒A的益损值,第二个数值代表B的益损值。A猜测B倒底是招还是不招呢?如果他招我不招,那么我就得接受惩罚而他会免除坐牢。奶奶滴,我可不能让他独占便宜,要坐牢咱一块儿坐!B可能也会这么想。嫉妒乃人之天性,我不好你也别想好。数学家这么解决这个问题?当然是假设信息对称,一个简单的假设是二个囚徒招认与不招认的概率各为50%。这样以来,从A的角度来说,他在“否认”栏的期望收益=1*0.5+(-1)*0.5=0,而在“招认”栏的期望收益是2*0.5+0*0.5=1。由对称假设,B的二个期望益损值与A相同。由于二个囚徒都认为招认的期望收益值最大,所以二个都招认,这就是Nash均衡点。为什么这是均衡点?那是因为每个人在这个决策群里的决策不依赖于别人的决策而变动,是稳定的;每个人的决策不仅不依赖别人的决策而改变,且大家都汇集到一个决策点,所以是均衡点。讽刺的是,在这个均衡点。二个人的收益都是零,即(0,0);也就是说,这个均衡是一个坑!
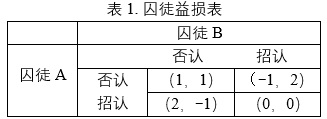
2. 带矢量损益的博弈论模型与大陆台湾在台海冲突里的应用
从表1我们可以看出,Nash囚徒困局里的均衡点取决于很多因素,包括对称性假设、益损估值等。而在很多实际博弈里,益损值不是一个简单的数值,而是一个多目标的矢量。本文试图把决策树和矢量益损结合起来,发展一个新的模型。为了直观起见,我则用台湾海峡特别是远东的潜在军事冲突作为入口,来阐述本模型。
1) 中国大陆与台湾单独军事博弈有没有Nash均衡?
大陆与台湾单独军事博弈只是一个假设,我只是把它作为后续分析的引子。但是,这个假设有一定的发生概率。台湾与中国大陆单独军事博弈,其损益矢量可能包括众多的内容,比如一旦发生大陆武统台湾的战争,就目前甚至今后相当长的时间内,毫无疑问台湾被征服只是时间问题。按我在“台湾与第三次世界大战”和“台湾的小牛和豪猪战略”文章里说的,2027年后某年大陆具备数小时内瘫痪甚至消灭台湾绝大部分武器系统的能力,几天内甚至24小时内能控制台湾的主要部分【1,25】。具体来说,台湾的益损类别可以初步估计如下。
1.1)台湾的短期和中长期益损
我们所说的短期,也就是从假设的大陆武统或逼降开始算起,大概二年左右。中长期则从大陆武力征服或台湾投降二年后记算。
1.1.1)台湾在大陆突然袭击下武打到底的益损
我们定义在大陆突然袭击武力征服台湾而台湾武力抵抗死拼到底, 以至于台湾军队消耗殆尽为状态1(State1), 并用Vt(1a, 1b,1c,1d,1e, 1f,1g,1h,1i)速打来表示其博弈益损矢量。该矢量里面各分量的初步分析总结如下。
1a) 台湾军人的伤亡:如果台湾拼打到底,军人大规模死亡是肯定的,其首脑如果不逃跑,则有可能被斩首【26】。假设台军全部战斗到最后,则军人伤亡数为约20万左右。这二十万大致是目前台湾正规军人数加上约20%的后备役人数【27】。其他民众伤亡暂时不计。
1b) 台湾军事设施、装备和弹药的损失:短期来说,台湾的军事指挥机构大概率会被中国PLA炸毁。外媒估计中国军方有三千以上甚至万辆火箭发射车,而中国气象局则隐藏有众多的气象火箭发射器可用于攻打台湾,台湾西海岸防御工事和武器以及水面舰船极大概率被大陆火箭消灭殆尽,大炮火箭几乎没有反应就被瘫痪或毁灭【28-31】。坦克和其它战车部分被炸毁。隐藏于山洞里的战机可能大部分免于炸毁,但是洞口及其附近跑道被大陆导弹毁坏而不能起飞,最后成为PLA的战利品。除了极少数高度抗干扰的导弹防御系统外,台湾估计来不急有太多的弹药投放。 中长期来说,台湾失去自己的军队,而由大陆PLA取代。
1c) 台湾的经济损失:按布隆伯格近期的专题研究,台湾在武打征服下经济下降最多可能达40%【32-33】。我们假设台湾被武力征服后短期经济下降40%,长期会恢复到某种程度,但是难以恢复到目前的高位。 出口中断,由于大陆武打破坏部分民用设施,台湾恢复普通性出口大概得一年左右。但是岛内高端芯片的制造和恢复估计机会不可能,因为其设计和制造的基础软件的控制权在美国等国家手里。我们还假设大陆在2027年后开始武打,那么介时台湾部分高端芯片制造力应该转移分散到安全国家去了。
1d) 台湾的基础设施损失:包括公用工程在内的主要基础设施可能部分受大陆的网络攻击而失去效能,假设有一小半被导弹和火箭弹炸毁, 一小部分被无人机毁坏或瘫痪。机场大部分被炸毁以防止权贵们大规模逃离和关键文件流失。但是我们假设这些被炸毁的设施由中国大陆最终买单。在大陆占领后建立傀儡政权后恢复秩序,修复被损坏的基础设施,全部完成估计得三年。
1e) 政府机构损失:中华民国政府和绿营领导人可能被斩首。民国政府和某些绿营地方政府大楼被炸毁。 最后也由中国大陆买单来重建。
1f) 自主领土:完全失去。
1g) 民众的心理:因失去领土和自由民主,愤怒和创伤十分严重。
1h) 领导人的尊严:如果死战则在自己和后人心里保持尊严,甚至有某种荣耀。这是一种个人心理感受且难以用金钱衡量的价值标准,但是有不少人会选择这么做以维持尊严。
1i) 中长期政治风险。因为我们认为在只有大陆和台湾二者军事博弈情况下,台湾中长期是大陆的一部分,所以它没有独立的中长期政治风险可以评估。
1j) 其它损失暂时不计。
1.1.2) 大陆突袭而台湾马上投降的益损
我们定义在大陆突然袭击武力征服台湾而台湾尽快宣布投降,以至于台湾军队人员和武器仅部分损失为状态2(State2), 并用Vt(1a, 1b,1c,1d,1e, 1f,1g,1h)打降来表示博弈益损矢量。该矢量里面分量的初步分析总结如下。
很显然,台湾被大陆突然袭击后不战而降的话 ,除了大部分台湾人民的愤怒和心理创伤以及台湾领导人的尊严丢失殆尽外,其它分量和武打致死相比,都明显占优。比如不会死去约20万台军,经济不会受到那么大的损失,且经济恢复更快。自主领土权总是要被大陆夺走,所以1f) 分量与速打到底持平。如果台湾对心理创伤和领导人尊严的注重低于其对伤亡和经济损失的注重,没有“不自由毋宁死”的气概,于是我们可以得出如下不等式(1):
![]()
该不等式说明,在只有大陆和台湾二方军事博弈的情况下,台湾被突然袭击后投降的益损矢量统治其拼死战斗的矢量 (Pareto dominance)。
1.1.3)大陆逼降而台湾拼死抵抗的益损
我们定义大陆逼降而台湾选择对抗到底为状态3(State3),其博弈矢量为 Vt(1a, 1b,1c,1d,1e, 1f,1g,1h,1i)逼打。其结果应该和大陆突然袭击而台湾抵抗到底的结果有所差别,比如台湾可能有些时间准备应战,其战机可能部分随时待命,潜艇进入关键的攻击位置,多杀死一些大陆空降兵,等等。但是,由于双方军力差距太大,台湾不会主动攻击大陆的政府机构和军事基地,而只是准备反击,其最终军事结果和State1相比略嘉(用符号≈≥表示),经济损失和进出口中断等方面都上与大陆速打后的状态没有什么差别。 所以,下面这二个不等式(2)和(3)是成立的。

1.1.4) 台湾在大陆逼降时先打再降的益损
我们定义大陆逼统而台湾先选择有限武力对抗,在失败后再选择投降的状态为State4,其益损矢量可以用Vt(1a, 1b,1c, 1d,1e,1f,1g,1h,1i)逼降 来表达。该矢量的各分量里,除了丢失主权相同外,都比“打降”、“逼打”、”速打“要好。台湾对抗到什么程度为嘉?当然是意思意思而不受实质性的损害,因为我们假设台海军事博弈只有大陆和台湾二方,台湾在没有终极致命武器情况下不敢肆意反抗,否则会导致大陆更血腥的打击。所以,如果台湾对心理创伤和领导人尊严的注重低于其对伤亡和经济损失的注重,没有“不自由毋宁死”的气概,下面这个不等式(4)是成立的。
![]()
结合公式(2-3),于是我们可以得出如下不等式(5)和(6):
![]()
从公式(5-6)的结果来说,台湾小打后再投降是其Pareto最优解【10,23-24】。
1.1.5) 台湾在大陆逼降时马上投降
很显然,台湾被大陆武逼且不战而降的话 ,除了民意愤怒和创伤严重外,领导人的尊严也会丢失殆尽。但是,与大陆讨价还价要求民主自由虽然不可能,但台湾领导人投降后可能被授予国家副主席之类的闲职和优厚的物质待遇。台湾益损矢量其它分量和武打致死相比,都明显占优。比如台军伤亡数不仅会低于对抗到底,也会大大低于State4里小打后降的数目。经济不会受到那么大的损失。自主领土权总是要被大陆夺走,所以1f) 分量与死命拼打持平。但是我们认为这是不可能出现的状态,因为台湾民意很厌恶大陆的威权政治和霸凌。台湾领导人如果这么做不仅会被耻笑,还可能被推翻。当年满清的康熙皇帝征服台湾时,郑克爽也是开始抵抗了一下,然后才宣布投降的【34】。
1.2)大陆中国的短期和中长期益损
大陆中国武打或逼困台湾的情况是与台湾的情况互动的。所以我们也用同样的四个状态来分析其在每个状态下的益损。
1.2.1)大陆突然袭击式武打且台湾死命抵抗后征服成功
我们把大陆中国在这种情况下的益损矢量用Vd(2a, 2b,2c,2d,2e,2f,2g,2h,2i)速打来表示。下面给出我们对此的初步矢量分量分析。
2a) PLA军人的损失: 由于大陆是突然袭击方且先远程用众多的导弹、火箭弹、无人机来投放弹雨,且台湾来不及有规模的反击,在大陆没有登上台湾岛时则没有或很少有PLA军人死亡。因为假设台军拼死战斗,在预估大陆空降5万和海渡15万先头部队后,估计台军剩余势力能消灭其中的40%,计8万人,伤者可能更多。 比美国CSIS于2023年模拟的PLA损失多出7万多【27】。但是大陆后续部队会源源不断开进。
2b) PLA军事设施、装备和弹药的损失:PLA军事指挥机构大概率会完好无损。其东海岸防御工事和武器以及水面舰船基本无损。运进台湾的支持先头部队的约五千辆轻型坦克、战车和摩托车预估50%被毁灭,10%自己抛锚。弹雨后出动五千架次无人机侦察和轰炸、二千架次战斗机轰炸机轰炸台湾和截击少量台湾升空战机,假设10%被击毁,3%故障坠落。
2c) 大陆的经济损失:前二年经济下降高达约16.7%【32-33】。其后很可能与发达世界隔离多年,经济很可能回到毛泽东时代的贫困落后状态。大部分出口受到西方的一致制裁而中断,但对俄罗斯阵营的进出口可能有些增加。大陆2022年出口3.59万亿美金,其中50亿美元以上的国家有67个,额度为$3347亿【35】。除去对俄罗斯阵营、中东和伊朗以及某些非洲国家的出口,还剩约$3194亿是对民主国家的出口。一旦大陆强势武打台湾,估计其第一年外贸损失高达85%约合3万亿。其进口额2.71万亿则会下降差不多的水平或更多,比如俄罗斯能源供给增加但是弥补不了中东失去的缺口。恢复对西方的进出口则遥遥无期。大陆在海外的投资和外汇有可能被没收,用来补贴流离失所的台湾人。
2d) 大陆基础设施的损失:主要基础设施无损。但是大陆武统成功后得出资修建其损坏的台湾基础设施。这样的战争次生费用必须得考虑进去。
2e) 政府机构损失:中华人民共和国领导人没有损失,中央政府大楼无损或略微损坏,福建浙江上海政府大楼局部损坏(假设台湾潜艇有部分反击能力)。
2f) 领土益损:因统一台湾,大陆获得领土和领海。也获得海军舰艇出入的隐蔽性。
2g) 民众心理益损:因统一而兴高采烈者众。但是因随之而来的经济严重下降导致大部分民众的心理创伤甚至愤怒。
2h) 领导人尊严: 因统一台湾,其领导人在短期里在大陆声望和荣耀增加。长期来说这些武力征服台湾的领导人可能会被认为是野蛮人。经济下行时间一长就使民众怀疑其攻打台湾的价值,认为得不偿失,抱怨领导人则会发生。不满情绪可能发生,甚至产生内乱。
2i) 大陆速打后中长期政治风险:由于西方联合制裁导致经济严重下滑且难以恢复,民众怨气逐步加大。政府信誉和领导力下降,内部矛盾大增,可能发生政变导致大屠杀行为。严重的可能危及到中共的生存,导致改朝换代。到头来所谓的民族复兴则是一场黄粱美梦。中国历史在秦始皇实行封建大一统后就是一个不断改朝换代的血腥历史。如果中共领导人能认识到这样的中长期政治风险,它就不该有任何武力征服台湾的行动。但是,我们认为大陆中共领导人认识不到这样的中长期政治风险,他只考虑短期的冒险收益,误判贯穿于中共执政后的历史,比如参与朝鲜战争导致与发达世界隔绝达近30年。他们甚至不能预计5-6年之后的事件演变,比如在约6前开始改变法律搞终身制和左倾独裁时,就没有预计到现在外企规模性供应链转移和部分民企出逃的结果。
2j) 其它损失暂时不计。
1.2.2)大陆突袭武打台湾而台湾马上投降的益损
这种情况对应于State2。我们可以把这种情况下大陆的益损矢量用Vd(2a, 2b,2c,2d,2e,2f, 2g, 2h)打降 来表示。假设大陆在发动第一波导弹和火箭弹雨后,台湾马上宣布投降。这样一来大陆派兵进驻台湾不会有很多死亡,也会减少弹药消耗和更多的设施损坏。其它分量如领土收益、经济损失、政治风险等与1.2.1相同或更优。也就是说,在如此假设下,下面的不等式(7)成立。
![]()
1.2.3)大陆逼降但是台湾死命抵抗
大陆逼降可能由很多种方法,包括巡航台湾四周,检查进出口船只并没收它认为违反其进出口规定的货物。宣布整个台湾为其防空识别区, 甚至夺取金门岛屿。这就是封锁,有些研究认为这对台湾有锁喉的效应。对于封锁战略及其后果,不仅中国自己多次研究,国际研究也很多,且有相当部分认为这是中国大陆比较可行的战略或策略,虽然美国政府和军方一再声明中国不可能封锁成功【36-42】。但是要破解PLA对台湾的封锁,则需要比传统武备更多的非对称手段【43-44】。美国资本家则留恋中国大陆市场,明里暗里支持中国夺取台湾,这表明了资本与自由民主的非同质性【45】。台湾如不屈服投降,则只有拼命死打到底。这种情况对应于State3。我们可以把这种情况下大陆的益损矢量用Vd(2a,2b,2c,2d,2e,2f, 2g, 2h)逼打来表示。在这种情况下,大陆最终还是要在合适的时候突然袭击全面进攻。其最终结果估计State1里开始就突然袭击武力征服相比要略差,所以我们得出如下公式(8)。再者,大陆消耗的时间可能稍长一些。
![]()
![]()
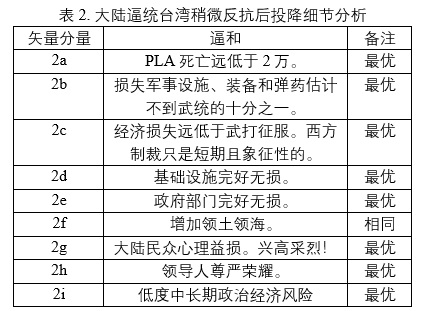
1.2.4)大陆逼统台湾稍微反抗然后投降的益损
此情况对应于State4。我们可以把这种大陆逼降的益损矢量用Vd(2a, 2b,2c,2d,2e,2f, 2g, 2h)逼降 来表示。我们也对其分矢量逐个分析,并把分析细节列入表2。
显然,对大陆来说,大陆逼降成功的矢量分量大部分大大优于、个别至少等于其它三个矢量的相应矢量分量(Pareto dominance)。于是我们得出如下不等式(9-11)。

1.3)短期决策树、矢量益损表和Pareto-Nash均衡
在只有中国大陆和台湾军事博弈的情况下,大陆毫无疑问是主动方。按博弈论的说法,是第一作动者(First mover)。台湾,特别是在没有美国民主世界的军事支持这个假设下,当然是被动方,处处小心谨慎防止冲突和战争。博弈树的设立也是按照这个思路进行的。
1.3.1) 大陆和台湾军事冲突的博弈树分析
此博弈树及其分析并不是一种预测工具,而只是一种研究手段,用于解释和探索概念。这个博弈树可以简单地以图1来表示。它主要是根据前面的二个重要假设,即台海军事冲突只有大陆和台湾二个博弈方,大陆领导人认识不到且不顾及中长期的经济政治风险。所以,大陆肯定会征服台湾,只是看看哪种方式费效比最好,同时满足大陆威权统治者的野心 (他们自己认为是荣耀)。 图1表示一个简单的三步博弈决策步骤,第三级表示短期的最终结果。中间可能还有很多子步骤,但是我们假设它们对最终结果没有太大影响。其相对应的博弈表可以用表3来表达。 为节省此节的篇幅,我忽略矢量里的分量。
如果抛开对各个状态State的概率估计或假设,那表4有没有一个纳什均衡呢?显然State4是纳什均衡。这是因为对台湾来讲,如果只有它和大陆进行军事博弈,那最佳策略就是选择投降。这是因为其包含8个矢量分量的四个博弈策略里,不管大陆采取是武打还是逼降,台湾象征性抵抗后投降是Pareto意义上的最佳策略(公式(5-6))。 同样,对于大陆来说,其四个策略里,由公式9到11确定,逼降的策略是最佳策略,且最佳策略也在表3的State4。所以我们断定State4是纳什均衡, 也可以称为Pareto-Nash均衡。我们没有赋予概率来确认纳什均衡,这是因为我们是研究一种政治军事行动大事前的博弈演绎,权衡各个策略的益损,以备用于制定后续的政治军事计划和政策的参考。


但是,这个均衡是在如下主要假设情况下推演出来的:如果台湾对心理创伤和领导人尊严的注重低于其对伤亡和经济损失的注重,没有“不自由毋宁死”的气概;大陆领导人不顾及武打台湾的中长期政治经济风险。这个假设与下面的无差别概率设定(50%对50%)有一致性。
我们先假设大陆突然袭击速打和逼降的概率各为50%,则台湾拼打和投降的期望矢量分别表达为公式(12)和(13):

由公式(5)我们知道,Vt(1a, 1b,1c,1d,1e,1f,1g,1h)逼降 >>Vt(1a, 1b,1c,1d,1e,1f,1g,1h)逼打。由公式(6)我们知道, Vt(1a, 1b,1c,1d,1e,1f,1g,1h)逼降 >>Vt(1a, 1b,1c,1d,1e,1f,1g,1h)速打 。考虑到公式(2)里的约等于号和前面所述的大于大于号,去掉一个大于号来弥补约等于号(≈≥)里微小的不确定性, 我们可以得出如下不等式(14):
![]()
于是我们亦然断定台湾投降的期望值大于其死命拼打的期望值。如果假设台湾投降和抵抗的概率各为50%,大陆速打和逼降的期望矢量分别表达为公式(15)和(16):

由公式8-11,引用我们上面的推论,我们同样可以得出下面的不等式(17):
![]()
在此情况下,大陆依然选择逼统而不是一开始就突然袭击狂轰滥炸,以至于台湾死伤无数基础设施毁坏严重。当然,如果极大改变概率分布,双方的策略会有所改变,其结果也随着改变。请看下面的分析。
现在我们改变假设:如果台湾对心理创伤和领导人尊严的注重远高于其对伤亡和经济损失的注重,完全具有“不自由毋宁死”的英雄气概,则几乎排除了投降之前提。则公式(2)、(4)、(5)、(6)都不再成立。如果我们亦然假设只有大陆和台湾参与台海的军事博弈、大陆领导人不顾及中长期政治经济风险,且大陆决策者没有台湾决死对抗的准确信息甚至还假设台湾决死对抗的概率无异于投降的概率,那么,表3的军事博弈则缩减为表4。这样以来,台湾的Pareto优势解是State3里的Vt()逼打,大陆最终的Pareto优势解是State1里的Va()速打。由于它们不在同一个状态, 所以不构成Nash均衡。

1.4)小结
本前篇充分论证了用矢量分析台湾和中国大陆政治军事博弈里的有效性。它不需要对每个矢量分量的全部详细计算来实现某种博弈策略对另外一种显著差异策略的Pareto优劣评估,从而发现优势策略和Pareto-Nash均衡。在只有大陆和台湾参与的台海军事博弈里,如果大陆不考虑武统台湾的中长期政治经济风险,且台湾没有坚决的抵抗意志,那就有一个Pareto-Nash均衡,即在大陆的逼迫下台湾稍微反抗后投降,以保全台湾的人命和经济。这个均衡也就是曾经演绎过的康熙-郑克爽博弈均衡。事实上,台湾民意测验表明,台湾民众对抵抗大陆武力入侵缺乏信心,大部分认为二方实力差距太大,台湾坚持不了多久【27】。
参考文献
【1】ZYuCannon , “台湾与第三次世界大战”,华夏文摘快递,2021年6月1日。
【2】A. Mccoy, “The Devastating Consequences of a War Over Taiwan”, The Nation Magazine, March 7, 2023.
【3】T.R. Heath, W. Kong, A.D. Huang, “U.S.-China Rivalry in a Neomedieval World”, Rand Report, Jun 6, 2023.
【4】Michael Gallagher, “Don’t Count on Economic Woes to Deter China”, Wall Streel Journal,Nov. 28, 2023.
【5】M. Shelborne, “PACFLEET CO Paparo Warns a Weak U.S. Maritime Sector Risk in Conflict with China”, USNI News,Feb. 1, 2024.
【6】M. Martina, D. Brunnstrom, “CIA chief warns against underestimating Xi’s ambitions toward Taiwan”, Reuters,Feb. 2, 2023.
【7】《增广贤文》里有警句曰,人群似纸张张薄,世事如棋局局新。
【8】苏格拉底言论集。
【9】维基百科:马奇诺防线词条。
【10】维基Cournot词条:https://en.wikipedia.org/wiki/Antoine_Augustin_Cournot。
【11】维基Stackleberg词条:https://en.wikipedia.org/wiki/Stackelberg_competition。
【12】Federal Trade Commission, “FTC Sues Amazon for Illegally Maintaining Monopoly Power”, FTC Press release, Sept 26, 2023.
【13】维基John von Neumann词条。
【14】John von Neumann and Oskar Morgenstern, Game Theory and Economic Behavior, Princeton Press, 1944.
【15】Britannica, Nash Equilibrium, https://www.britannica.com/science/Nash-equilibrium.
【16】N.G. Mankiw, Principles of Economics, 10th Edition,
【17】Open Yale Courses, ECON 159, Game Theory, Lecture 8 – Nash Equilibrium.
【18】Hailun Li, “Game Theory for Analyzing China-Taiwan Relations”, 2020 8th International Education, Economics, Social Science, Arts, Sports and Management Engineering Conference (IEESASM 2020).
【19】C. Blattman, Why We Fight: The Roots of War and the Paths to Peace, Viking, 2022.
【20】S.L. Quackenbush, “Game Theory and Interstate Conflict”, Oxford Biographies.
【21】P. Dizikis, “What game theory tells us about politics and society”, MIT News, Dec. 4, 2018.
【22】D. Snidal, “The Game Theory of International Politics”, World Politics, Vol. 38(1), Oct 1985, pp 25-57.
【23】 P. Samuelson and W. Nordhaus, Economics, 19th Edition, McGraw-Hill Irwin, 2010.
【24】J. Gruber, “Principles of Economics – Lecture 13: Oligopoly”, MIT OpenCourseWare, 14.01, Fall 2018.
【25】ZYuCannon,“小牛与豪猪战略-台海共赢思考之二”,华夏文摘快递,2023年2月27日。
【26】“軍迷揭內蒙靶場似台北特區 台防長:彰顯斬首戰企圖”, 明报新闻网,2024年3月28。
【27】台湾民调:过半人不信能抵御解放军百日 – BBC News 中文,2022年6月22日。
【28】吕嘉鸿,“美国智库推演台海战争 若美日参战台湾将惨胜”,BBC中文,2023年1月12。
【29】钟辰芳,“日智库模拟2026年中国攻台,美日若涉入可阻遏北京但将承受重大损失”,美国之音2023年2月28。
【30】M.F. Cancian, M. Cancian, E. Heginbotham, “The First Battle of the Next War – Wargaming a Chinese Invasion of Taiwan”, CSIS Report, Jan 2023. Available at CSIS Website.
【31】科学知识点秀,“中国神秘武装力量,坐拥万台高射炮和火箭炮,战力碾压小国军队”,网易号,2022年8月19日。中国气象局有近万门火箭弹发射器,包括先进的SY-400!
【32】 J. Welch, J. Leonard, M. Cousin, G. DiPippo, T. Orlik, “Xi, Biden and the $10 Trillion Cost of War Over Taiwan”, Bloomberg special report, Jan 8, 2024. US6.7%,World10.2%
【33】S. Kuper, “Assessing the true cost of a Taiwan conflict”, Defence Connect, Jan 12, 2024.
【34】维基百科,“康熙定台”词条。
【35】Trading Economics: China Exports By Country (tradingeconomics.com)。
【36】M. Jesrtab, “A maritime blockade of Taiwan by the People’s Republic of China: A strategy to defeat fear and coercion”, a report, Atlantic Council,Dec. 12, 2923.It claims that blockade is the most strategically viable option for the PRC.
【37】C. Buckley, P. Robles, M. Hernandez, A.C. Chien, “How China Could Choke Taiwan”, New York Times, Aug. 25, 2022.
【38】G. Dominguez, “As invasion fears rise, China hones Taiwan blockade strategy”, The Japan Times, Oct. 3, 2023.
【39】C. Vickers, “Crisis in the Taiwan Strait likely in 2024, experts say”, THE HILL, Jan. 22, 2024.
【40】J. Seldin, “US Warns China Cost for Blockading Taiwan to be Very High”, VOA, Oct. 5, 2023.
【41】 “Chinese blockade of Taiwan would likely fail, Pentagon official says,” Reuters, Sept. 19, 2023.
【42】唐缘媛,“今年中国会对台隔离、封锁还是进攻?逾80位学者给出答案”,RFA, 2024年1月22日。
【43】H. Brands, Z, Cooper,”Dilemmas of Deterrence: The United States’ Smart New Strategy Has Six Daunting Trade-offs”, CSIS report, March 12, 2024.
【44】J. Blanchette, B. Glaser, “Taiwan’s Most Pressing Challenge Is Strangulation, Not Invasion”, WAR ON THE ROCKS, Nov. 9, 2023.
【45】Reuters, “Taiwan blasts Elon Musk over latest China comments”, Sept. 13, 2023.
(作者版权所有,引用请注明出处。谢谢!2023年3月31日完稿)
作者投稿

 参加论坛上关于本文的讨论
参加论坛上关于本文的讨论