最近有位网友L发了一篇关于债券投资的散文。虽然另有网友S友情提示文章不足之处，但是，in a respectful way, L是位经典的“话粗理不糙”的模范，而且其本人的谦虚态度在傲慢爆表比比皆是的CND上的确是难能可贵的。一看就知道L是个谦虚好学的君子。
咱现在也写篇简单的硬货烘托烘托，聊聊债券领域的两个基本元素 ––债券定价与久期 (Duration)。咱将数学概念应用到现实世界的交易数据，希望读者看了本文以后能弄清楚债券交易的来龙去脉。
一、债券定价 (Bond Pricing)
下图是 2/23/2024 CNBC上美国十年债券 (10-Year US Treasury Note) 的交易数据。从图中可以看到一些必要的数据 –– 市场 Yield-To-Maturity (YTM) = 4.248%，即投资者如果买了这个 T-Note 并 Hold到10年期满，那么她最终的投资回报率就是这个数，这就是为什么债券是固定收益产品 (Fixed-Income Product)；价格 Price = 98 (par price = 100 was implied)；Coupon Rate = 4%。
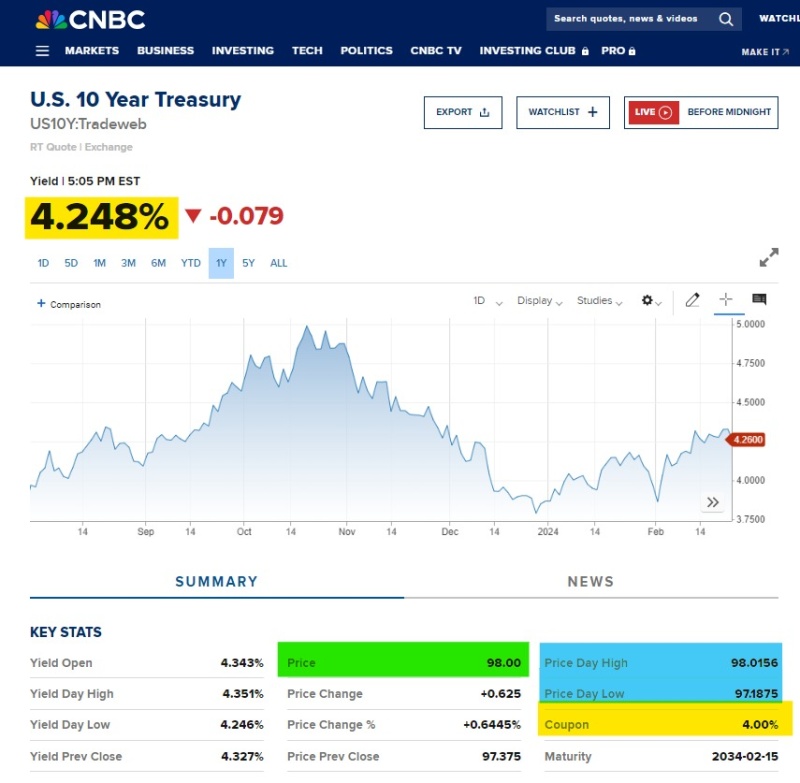
图一
债券的定价公式推导是相对简单的一个数学过程，即将所有的未来现金流 (Cash Flow)，此处即为债券的 Coupons，discount 到今天便是它的价格。有一个投资者必须记住的惯例 (Convention) 是债券，尤其是政府债券的 Coupon 是半年 (6个月) 发一次的。所以数学公式里通常是将 Maturity 乘以2，得到 Periods of Coupon Payments，同时 Coupon Rate 和 YTM 都要除以2，得到每个阶段的 Rate 或 Yield。具体公式就是：
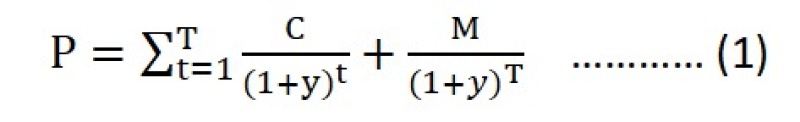
其中 C 是每期的 Coupon （为简单记，假设它是个常数，因为通常美国政府不会赖账，在到 Maturity 之前降低 Coupon Rate 甚至 Default 耍赖，至少现在可能性还小，将来就不知道了），并且 C = Coupon Rate/2×M = r×M, M 为债券的maturity value (收回面值)，此处为 par value = 100。公式里 y = YTM/2。T= 2×Maturity，对10年 T-Note 来说，T = 20。
方程 （1） 里的第一项是个等比级数，经过简单推到，方程就变成如下的简洁形式。
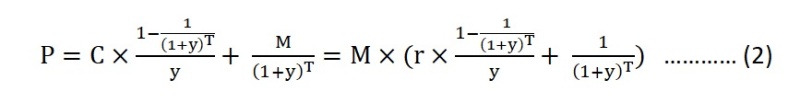
下图二 （Price-YTM）的美国10年期 T-Note 价格/YTM 曲线便是根据方程（2）和 图一中 CNBC 2/23/2024 的交易数据制作的。从图中可以看出，在市场主导的 Yield-To-Maturity (YTM) 4.248%, the 10-Year T-Note 价格在精确到小数点后两位数的情况下，计算值与市场交易价格完全吻合。图中还插入了一个列表。它在下面的讨论中有用。
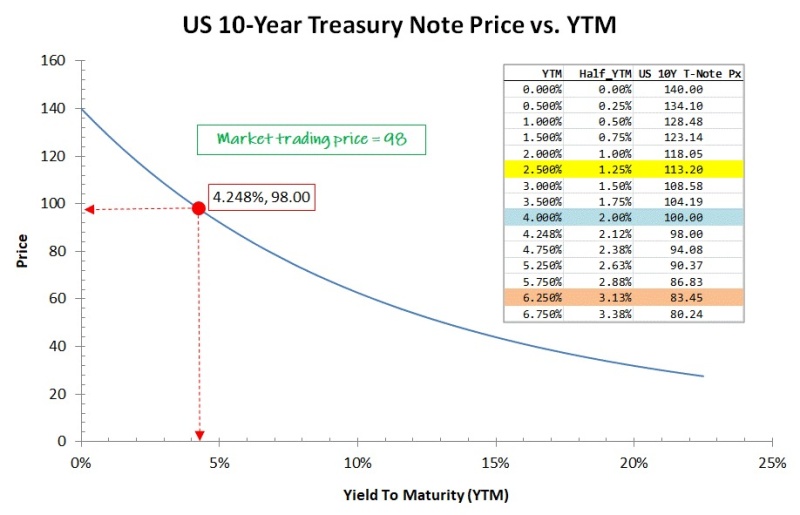
图二
从CNBC 的交易数据图和这个 Price-YTM 图中的插表可以看出，因为 YTM 4.248% 高于 10-Year T-Note的Coupon Rate 4%, 所以它成了降价债券 (Discount Note), 即价格 98 低于它的 Par Value 100。在此前不久美国10年期债券还是 Premium Note 呢。这说明它现如今面临供过于求，很难轻轻松松地割韭菜的悲惨境界了。作为一个 Premium Bond （Note in this case as the maturity is 10 years; naming convention: maturity within a year is called a Bill, 1-10 years maturity is called a Note, beyond 10 years maturity is called a Bond）的 Hypothetical Case, 假设现在的 YTM = 2.5%，对照图中的列表，你可以看出与之对应的价格是 113.20，即因为 YTM 低于 Coupon Rate 4%, 这种情况下的 10 YearT-Note 的价格高于它的 Par Value 100。这些分析的结论也可以从方程（2）中解析地得出，只要将不同情况下的 Coupon Rate (Rc=2r) 与 YTM (=2y) 的大小关系代进去就行了。简单地总结一下便是，如果 y 大于 r, 它就是 Discount Note；如果 y 小于 r, 它就是 Premium Note；如果 y 等于 r, 那它就是 Par Note, 在这种情况下，方程（2）就退化成 P=M, 这正是我们期待的。
二、债券久期 （Bond Duration）
Bond Duration 在 Fixed-Income投资管理中是非常重要的一个概念和指标。这个主题里有各种各样的 Durations，而在咱看来，其中的 Modified Duration算是最重要的了。后面咱会阐明为什么是这样。
首先咱们回到前面的方程（1）。如果我们将它两边都对 y 求导数，那么我们就会得到
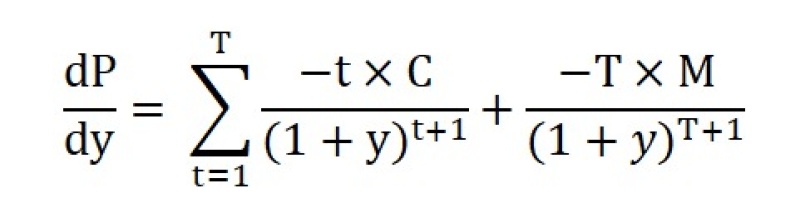
然后两边再除以 P 并稍加整理，提出一个公因子 （1+y）。那么，
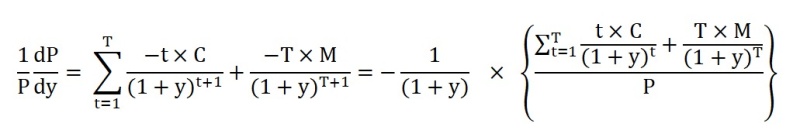
花括号里的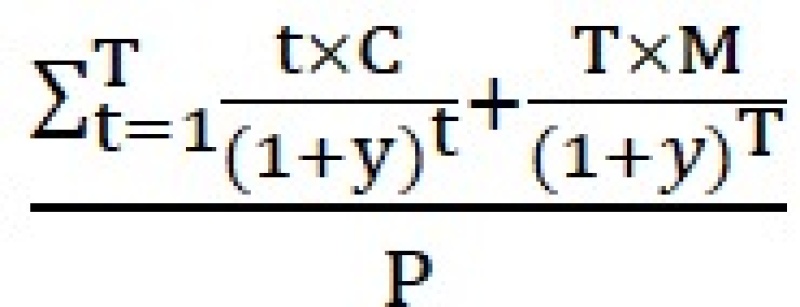 
项就是通常人们说的麦考利 (坊间称“卖烤栗”，well, 咱瞎编的) 久期，是由加拿大人Frederick Robertson Macaulay 于1938年推出发表的。咱们暂且把Macaulay Duration称为 MacD。其实MacD 本身没什么用，但是如果把那个 1/(1+y) 吸收进去，那世界就大变样了。人们把这个新玩意儿称作 Modified Duration (MD)。那么，
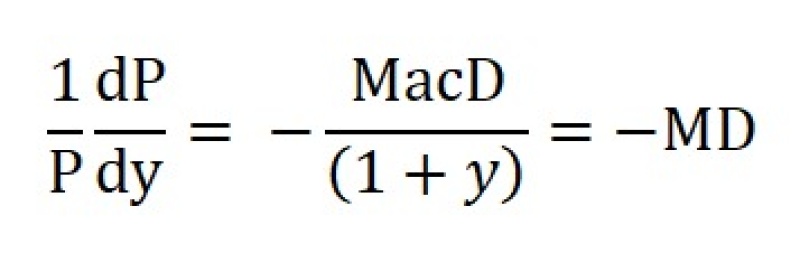
即，
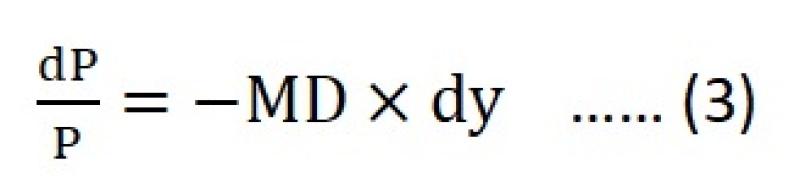
这可是革命性的量子飞跃。这一下债券世界就好解释多了。MD 就是当 Yield 改变 1%，也就是 100 Basis Points 时债券反方向的百分比变化。例如，如果 MD = 8 年，那么当Yield 增加 100 Basis Points 时，债券的价格就要跌 8%。换句话说，MD 是债券响应 Yield (interest rate) 变化的灵敏度的一个衡量标尺，MD越大（长），这个债券的 Volatility 就越大，反之亦然。所以 Fixed-Income Investors 经常用 MD 来比较不同的债券。因为 Fixed-Income Portfolios 的 MD 就是其组成债券的 MD 的线性加权和，使得 Bond Funds 之间的比较也相对容易。下面的三种情形下的列表展示了 Macaulay Durations (MacD), Modified Durations (MD) 的具体计算过程。从它们可以看出：（1）三种情况下计算出的价格与前面插图中的列表里的计算价格是相符的；（2）MacD and MD 都比 10-Year Treasury Note 的 Maturity (10 Years) 要短，而它们之间的差距并不太明显尽管随 YTM 缓慢下滑，都在8年左右。
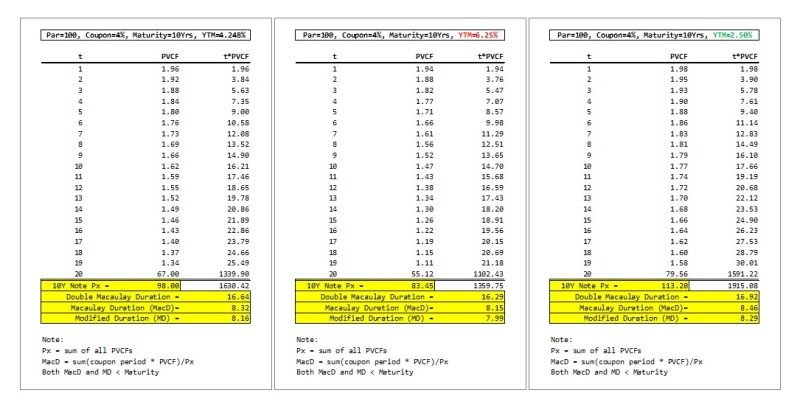
图三
三、非线性效应（Nonlinear Effects）
前面方程（3）dP/P = -MD x dy显示债券的百分比随 Yield 变化的关系是线性的。这说明，这个方程只对微小的 Yield 变化响应得较好。一旦Yield 变化巨大，那么这个方程给出的价格变化误差就特大了。此时，前来解围的便是 Fixed-Income Investing中的另一个重要变量，叫做 Convexity。它是价格变化的二阶导数。它的应用咱就不在此多说了。感兴趣的咱们可以单聊。不过咱可以把数学推导放在这里作为结尾。其实也很简单，只要用一用泰勒级数展开就行了。
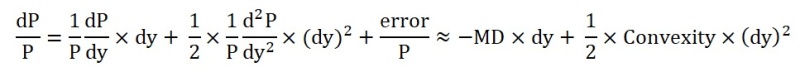
可以看出，对于通常的 (Conventional) 债券来说，Convexity 对债券价格的贡献总是正的，碰到Price-YTM 向下拐弯的（Concave），比如在 Callable Bonds的情形里，当 Yield 降到很低时，Price-Yield 曲线从 Convex 过渡到 Concave，它们的 Convexities 就会变成负数了。因为是二阶导数效应，从绝对值来看，Convexity 对价格的贡献通常比 Duration 的贡献要小得多，大概一个数量级左右。比如说，在咱们这个10 年T-Note 的例子里，MD = 8.16 年。假如 YTM 从4.248% 窜到 6.25%，根据前面Price-YTM 插图理的精确计算，其价格从98 瞬间跌到83.45, 即其变化为 -14.55。MD的贡献为 dP = -P*MD*dy = -98*8.16* (0.0625-0.04248)=-16。忽略三级效应，Convexity 的贡献仅为 -14.55-(-16)=1.45。比较一下，Convexity 的贡献仅为 Duration 的 1.45/16=9%，即十分之一左右。
债券市场曾经以它的枯燥乏味著称，名校金融专业的毕业生没人愿意选择那个职业，直到金融衍生物市场爆发。有趣的是，今天美国的债券市场 ($51 Trillion) 与股票市场 ($50.8 Trillion) 几乎一般大。但是，衍生物 (Derivatives) 市场就完全不一样了。尤其是 OTC Derivatives，据 Bank for International Settlements (BIS) 的最新报告，截至2023年6月，仅 Interest Rate Swaps 就有 $574 Trillion，也就是十倍于上面提到的美国 Plain Vanilla Bond Markets的大小。换个角度看，根据世界银行的最新数据，2022 年全球 GDP总额为 $100.88 Trillion。设想一下，如果 Swaps Markets Collapse，它们对全球金融市场和经济的冲击将会有什么后果。鉴于这个巨大量级的差异，有空咱再写一篇 Interest Rate Swaps 的小文，其中的数学当然要复杂一些，但是也扯不上危言耸听、可望不可及。 再说吧。
February 24, 2024
© Dr. CeeTee