The fruit of reinventing wheels when studying Euclidean geometry

1. Abstract

By studying in steps what a flat plane is, this paper shows that only six axioms are necessary for 2-dimensional Euclidean geometry until the Pythagorean Theorem: 1) the existence of stable space; 2) the existence of a straight line through any two points, 3) the existence of distance measurement between any two points; 4) the limitation of the space to 2-dimensional, 5) the repeated equivalence, and 6) the reflected equivalence.  

Besides introducing major mathematical concepts to young readers, this paper focuses on the context and thought process to conclude these axioms, and necessary theorems to test mathematically whether a 2-dimensional space is flat or not.  It can also be used as a short introduction to Euclidean geometry until Pythagorean Theorem. 

Copyright 2017Ó by ChengpuWang.

2. Purpose

The geometry on a flat plane has been studied by Euclidean geometry [1][2], which established the first complete scientific reasoning system [3] in our human history.  Yet, it is not easy to define a flat plane, because it requires the whole tool set for mathematics [4].  A peculiar observation is that the original definition of 2-dimensional Euclidean geometry [1][2] has no obvious axiom which is specific for properties on a flat plane directly.  Since 1960s, it has been well known that not all geometric objects on a flat plane are 2-dimensional [5] or Euclidean, so that it might be necessary to revisit the foundation for Euclidean geometry. 

To understand Euclidean geometry better, this paper will provide a thought process along the common four steps to study tangible objects in science:

1. Observations [6], where science starts.
2. Generalizations [7], which lead to either axioms [8] or definitions [9].
3. Deductions, which lead to theorems [10] and self-consistent checks [11] based on existing axioms, definitions, and theorems.  The deduction process itself uses mathematical logic [3] which may contain implicit [12] axioms or theorems from other branches of mathematics.
4. Applications, which lead to reality checks, measurements [13], and tests [14]. 

We will see what these concepts are when following these four steps during our discovery of what a flat plane is.  Our goal is to find a test [14] to judge whether a 2-dimensional space is a flat plane or not.

The main purpose of this paper is to show young students of mathematics the importance to peruse the thought process of mathematics within the context of the current curriculum of high school in the above four steps.  The benefit of such thorough study of the current curriculum is to preserve creativity in mathematics, think thoroughly, and develop the ability to ask good questions.  For any conclusion in mathematics, there are four levels of understanding: 1)  How to understand it? 2)  How to apply it? 3) How to prove it? 4)  How to come up with it? 

A thorough understanding consists of answering all these four questions, while the current curriculum of US high school only asks for 1) and 2) [15].  In the other extreme, best high school students of mathematics have been rushed into math competitions [16] or advanced courses in mathematics [17], ignoring the beauty in basic mathematics such as Euclidean geometry.  This paper will try to introduce Euclidean geometry from the prospect of answering 4).  For this purpose, this paper will use “we” to lead young students onto a path of discovery, and focus on how to come up with each axiom or theorem.  Instead of the common practice of giving a theorem then proving it, in most cases, this paper will use solid mathematical logic to lead to each axiom or theorem, with rigid proof of the theorem sufficient in the context—the importance of solid proof has not been compromised.  To benefit readers not proficient in mathematics, this paper will also use easily accessible and understandable references primarily from Wikipedia.

A 2-dimensional space is an important subject to study.  Because we are living in a 3-dimensional space, we can construct and visualize 2-dimensional space easily.  But we cannot always limit ourselves to such easy cases.  We need to characterize the 3-dimensional space which we are living in, such as to understand why and how our space-time can bend according to the theory of general relativity [18].  We also need to extend our knowledge beyond the space-time which we are living in directly, such as to understand string theory [19], which says that the world which we are living in is indeed 11-dimensional.  For the above purpose, we will imagine ourselves as 2-dimensional people within a 2-dimensional world, and find rules to detect whether we are living on a flat plane or not.  Such imaginations in science are called thought experiments [20], which are vital parts of scientific discovery.

We will see that by reinventing the wheel for reconstructing Euclidean geometry [1] [2] from the beginning, we will gain some insight into Euclidean geometry and mathematics.  In fact, we will result in an alternative set of axioms which seem more solid, understandable and reasonable.  Using Euclidean geometry as a showcase, we will focus on the concepts and creativity of mathematics in the thought process, rather than the techniques and advanced topics of mathematics.  Essentially, mathematics is about ideas, and logic relations between ideas, while techniques are just tools which can be mastered later when needed, especially for high school students.  Perhaps, if we study advanced mathematics in a hurry, we will lose a lot of chances to ask questions, and our ability to ask questions will suffer most.  So let’s try to find the answer to the question together: how to define a flat plane.

3. What do we study in Euclidean geometry?

As our first observation, in Euclidean geometry, we can understand the properties of one type of objects only if we know how to construct such an object anywhere using simple rules, such as a point, a straight line, a circle, a triangle, etc.  In fact, not all geometric objects in a 2-dimensional space are 2-dimensional.  For example, the accurate map of the British island has fractional dimension [5], which is beyond the scope of Euclidean geometry.  Thus, we will start from the following basic definitions for Euclidean geometry:

• A point denotes an existence at a fixed location in space but without any other properties.
• A geometric object is formed by a fixed set [21] of points.  If two geometric objects repeat each other point by point, they must be the same geometric object, and have same properties.
• A constructible object is a geometric object which can be uniquely constructed by a limited set of deterministic rules, so that if we run the rules for a constructible object twice, the resulted two constructible objects must be the same geometric object. 

Before we can study a space, we must make sure that the space is stable.  For example, if we are waving a paper so that it keeps on deforming, it is meaningless to see such a changing 2-dimensional space is flat or not.  A same geometric object can be constructed repeatedly and unconditionally only if it is in a stable space.  Thus, we assume:

4. What is (or rather what is not) a flat plane?

Actually in science, the most difficult question to answer is usually the simplest question to be answered, and we should spend most time pondering about it, which is contrary to current common practices in US middle and high schools.  A flat plane is such a case.  Let’s pretend that we know what a 2-dimensional geometric object is for now, and concentrate on how to define what flat means. 

If we cannot define or characterize a concept directly, perhaps we can work in the opposite direction by asking what it is not.  Let’s start with observation.  We know that a paper on a flat table is part of a flat plane.  Let’s see what we can do to make it no longer flat:

• We can fold it:  The folded line stands out, so it is special.
• We can bend it: The direction perpendicular or along the bend has a different curvature.

There must be some rules or operations that can distinguish these special place or direction, although we do not know what they are yet.  On the other hand, on a flat plane, there is neither any special place nor any special direction.  Thus, we will use the word any frequently, and we will use two axioms to specify that the space for a flat plane is homogeneous.  Such a requirement of space homogeneity without specifying how to achieve or verify it is called an ideal condition [22], which is frequently used in scientific theoretical studies.  Using homogeneity, we can exclude almost all types of 2-dimensional spaces, leaving only the spheres [23] and the flat planes to distinguish.  Such is the simplification process after idealization [22]. 

Visually, a flat plane and a sphere are different in two ways:

• Although both are boundless, a flat plane is infinitive in size, while a sphere is limited in size.
• A flat plane can contain straight lines, while a sphere cannot.

It is not practical to investigate if the size of the space is infinitive.  Using size limitation, we can only tell whether a homogenous space is a sphere, but not whether it is a flat plane, because logically, we cannot measure whether the size is infinite or not.  A more practical application is usually a better application of mathematics.  Let’s try to characterize the flat plane using straight lines.

5. Straight Line

Straight line is another such simple concept which is difficult to define.  We cannot give a complete definition to it, but we can characterize it by its unique properties.  To obtain such properties, let’s see how we can draw a straight line using a ruler [24]:

• The portion of the straight line that connects any two points is called a straight line segment and each of the two points is an end point to the straight line segment.  A ruler is an idealized [22] straight line segment which can be moved around on a flat surface. 
• Given two existing points, we can draw a straight line segment passing through them.
• Given an existing straight line segment, we can select two points near an end point, and extend the straight line segment beyond the existing end point, to produce a new straight line segment with a new end point.  Repeating this process, we can draw any straight line segment as long as we need, which approaches a true straight line.
• The uniqueness of the straight line passing any two points can be used to define distance between the two points, and it defines the shortest length along any path between the two points.
• If the ruler is not straight within the flat plane, we can draw at least two lines passing any two points using the ruler. 
• If the space itself is a sphere, we can draw a unique line passing any two points which has the shortest length on the sphere, provided that these two points are not opposite poles on the sphere, because there are more than one shortest path connecting a pair of poles.

Thus the uniqueness between any two points is indeed a unique property for straight line on a flat plane.  We can generalize our observation of a few cases as an axiom to all cases:

The word “one” in Axiom 2 implies that every straight line is identifiable and unique.  If all points are on a same straight line, then the space is 1-dimensional, so that the phrase “and only one” in Axiom 2 is no longer necessary.  Axiom 2 actually implies that the space is more than 1-dimensional which can contain more than one straight line.  The usage of language is important in mathematics.

Axiom 2 suggests that:

Theorem 1. A straight line can be constructed by any two points on the straight line.

Theorem 1 is essentially a restatement of Axiom 2 in a narrower context of selecting any two points on an existing straight line.  It provides the foundation why we can have a ruler as a tool to draw straight lines.  An alternative statement for Theorem 1 is:

Theorem 2.  If two straight lines shares any two points, they are the same straight line.

In our observation, for any three arbitrary points A, B and C, if C is not on the same straight line with A and B, then A is not on the same straight line with B and C.  Otherwise, assume: 1) C is not on the same straight line with A and B; and 2) A is on the same straight line with B and C.  Applying Theorem 1 to 2), the straight line can be determined by either A and B, or B and C, thus C must be on the same straight line with A and B.  The logical conclusion of 2) conflicts with the assumption in 1), so 1) cannot stand.  Using the above proof by contradiction [25], we have proven:

Theorem 3. For any three points, if one point is not on the same straight line of the other two points, then these three points are not on a same straight line.

From how it is proven, Theorem 3 is a restatement of Theorem 1 in a new context.  It shows that a proof contains important relations among axioms and theorems [4].

Two geometric objects intersect each other if they share points.  Axiom 2 is violated if two straight lines intersect each other at more than one point:

Theorem 4. If two straight lines intersect each other, they can only intersect at one and only one point.

If a straight line has any end, we can find another point on the straight line, and extend the straight line beyond that end according to Axiom 2.  This means that a straight line is endless and continuous: 

Theorem 5. A straight line is continuous and endless. 

Theorem 1, Theorem 2, Theorem 3, Theorem 4 and Theorem 5 all apply Axiom 2 in different context, and provides really nothing new, unlike Axiom 2.  Theorems exist because they are useful.

Theorem 1, Theorem 2, Theorem 3, Theorem 4 and Theorem 5 are obvious, or even trivial, from what we already know by observation.  By deducing them, we have performed reality checks for Axiom 2.  Historically, due to easy reality checks, Euclidean geometry was the laboratory for creating mathematical logic [3][4].  In addition, mathematical logic enables us to vision beyond what we can observe directly, such as bent space-time in general relativity, or geometry for higher dimensions. 

5.1 Distance

A ruler [24] has another function: to measure distance.  In fact, there are many definitions of distance, such as the metric system [26], the light-years [27], or in the linear scale [28], or in the logarithmic scale [29].  But in mathematics we usually do not care about actual distance values, but only the distance relations between different geometric objects.  For example, traditional Euclidean geometry has another tool called compass [30], which allow us to copy distance between any two points regardless of the actual value of the distance.  We can generalize the common properties of different distance definitions as a set of requirements for distance which is common for all distance definitions.  This is called abstraction [31] in mathematics. 

For any two points A and B, we will simply refer to the straight line segment that connects these two points as line AB.  Because it is “one and only one” according to Axiom 2, line AB can be used to define distance |AB|Î[0,¥)^R (as a non-negative real value [32]) which satisfies the following requirements:

• |AA|=0;
• For any two different points A and B, there exists a distance |AB|=|BA|>0;
• Any point C on line AB satisfies |AB|=|AC|+|CB|.
• Any line AB must contain one mid-point M which satisfies |AM|=|MB|=|AB|/2.

Because such requirement for distance may not exist in all 2-dimensional space, it is not sufficient [33] for its own existence.  We need:

Axiom 3 suggests that the space can be measured by distances.  To connect the objects being studied with measurements [13] is usually the one of the earliest steps in scientific studies.  In Euclidean geometry, we only need one measurement: the distance. 

From the requirement of distance:

Theorem 6. If |AB|=0, then A and B must be the same point. 

According to Theorem 6：

Theorem 7. If point C₁ and C₂ are both on line AB, and |AC₁|=|AC₂|, then C₁ and C₂ must be the same point. 

Apply this conclusion to the mid-point to any line:

Theorem 8. There is one and only one mid-point for any line segment.

If point C is on line AB, assume there are gaps with |AC|Î[0, |AB|]^R.  From Axiom 3, we can always pick two points around one gap, and simplify the problem as: |AC|Î[|AC₁|, |C₂B|]^R.  |AB|=|AC|+|CB| leads to |AC₁|=|C₂B|.  Such assumption means that line AB cannot contain a mid-point, which violates the requirements for distance.  Combing |AC|Î[0, |AB|]^R and Theorem 7:

Theorem 9. There is an one-to-one correspondence between a point C on line AB and a distance |AC|Î[0,|AB|]^R.

The requirements for distance could have used the content for Theorem 9 instead of the requirement for the existence of mid-point.  However the latter is preferred because it is more practical to test an actual distance definition for the requirement.  In mathematics simplicity is beauty.

5.2 Continuity

The requirement for distance should also be self-consistent [11], such as what type of number should be used for distance:

• If we defined distance as integer value [34], for any |AB|=1, we can always find a mid-point C on line AB so that |AC|=1/2.  We can immediately see that such a requirement is not self-consistent.
• If we defined distance as rational value [35], we cannot dispute it because we can always find another rational value between any two rational values, or another rational value larger than any rational value, as how we have proven Theorem 5, until we prove the Pythagorean Theorem [36] later, which requires the distance to be both rational and irrational [37].  Or a wrong definition or axiom can cause consistency problems later.

Thus, the choice of real value for distance suggests that a definition can also contain new information, implicitly or explicitly, also as a generalization of observations.  As a result, Theorem 9 is a quantification of Theorem 5 for the continuity of straight line, in which the usage of real value reveals the quantitative nature of such continuity. 

5.3 Ray

If a straight line crosses itself, it must form a loop according to Theorem 5.  The distance between any two points on the loop will no longer be unique, which violates Axiom 3. 

Theorem 10. A straight line cannot cross itself. 

We can use Theorem 10 to split a straight line into two rays by any point on the straight line, with the point called starting point for each ray.  A ray is referred by the starting point and any other point on the ray.  Using rays, Theorem 9 can be further simplified as:

Theorem 11. There is one-to-one correspondence between a distance Î[0,¥)^R from the starting point of a ray and a point on the ray.

6. Circle

Compass [30] has another important function: to draw a circle centered at any point for any radius.  A circle is the set [21] of all points which have a predefined distance called the radius from a point called the center.  From Theorem 11, circle exists.  A circle is usually referred to by its center. 

Between any point A and the center C of any circle with a radius of R：

• If |CA|<R, we can always extend the ray CA to point B until |CA|<R=|CB| according to Theorem 12, or point A is inside the circle C. 
• If |CD|>R for another point D, then there must exist a point E on ray CD so that R=|CE| according to Theorem 12, or point D is outside the circle. 

Thus:

Theorem 12. A circle intersects any ray starting from its center at one point, and divides the ray into two section of inside and outside the circle, respectively..

For two arbitrary circles A and B, if all the points of circle A are inside circle B, circle A is inside circle B, while circle B is outside circle A. Thus, a circle is a local object on a flat plane, while a straight line or a ray is not. 

6.1 Dimensionality

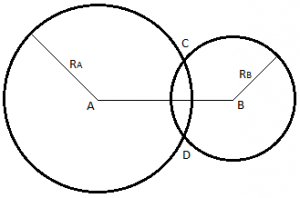
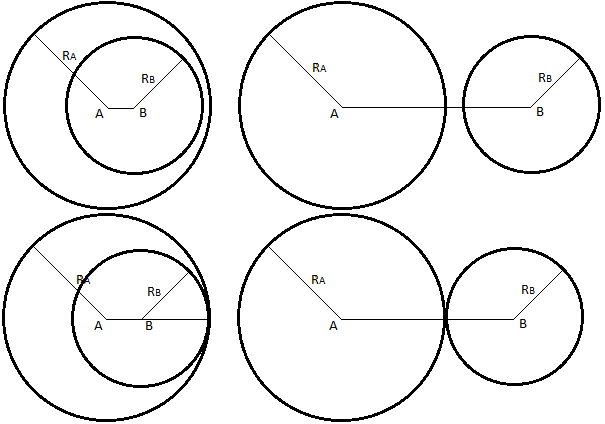
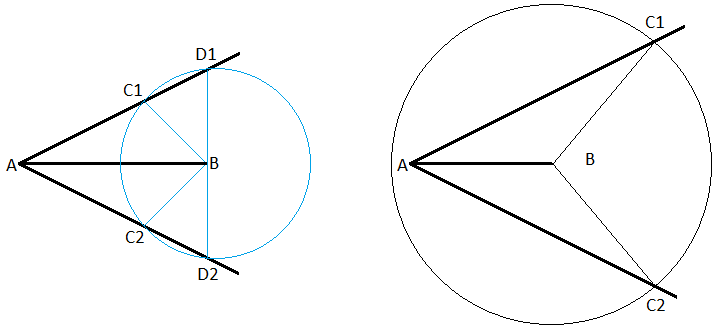
The above definition and properties for circle are actually dimensionless.  It could describe a circle on a 2-dimensional space, or a ball on a 3-dimensional space.  In fact, Axiom 2 and Axiom 3 have not stated the space dimensionality at all, and they are also true in 3-dimensional Euclidean space.  We need a new axiom to limit the space to 2-dimensional.  A straight line is always 1-dimensional, while the definition of circle can describe either a circle on a flat plane, or a ball in 3-dimensional Euclidean space.  A straight line is always 1-dimensional, while the definition of circle can describe either a circle on a flat plane, or a ball in 3-dimensional Euclidean space.  We need to find a context which only exists on a flat plane.  Obviously, we should start at the geometric relation between two circles.  By observing the relation between two circles in Figure 1 and Figure 2, we found that only the case in Figure 1 is unique in 2-dimensional space, because two balls may intersect each other at either a circle or a point in 3-dimensional space.  We can capture this observation in an axiom for the specific dimension:

Figure 1  Two circles intersect each other at two points.

Figure 2  Relations between two circles other than in Figure 1.

One immediate simplification of Axiom 4 is:

Theorem 13. For any three points A, B and C which are not all on a straight line, |AB|<|AC|+|CB|.

Axiom 4 actually defines “flatness”, at least partially:

• According to the definition for distance, when point C is on line AB, |AB|=|AC|+|CB|.  Combined with Theorem 13, a straight line has shortest path between any two points, which is a first description of “flatness”.
• According to Axiom 4, a straight line divides a flat plane into two separated sides, which is not true on a plane which is not flat, such as on Mobius plane[38].

Axiom 4 can further be extended to a few more cases in Figure 2:

Theorem 14. For any two circles which are centered at arbitrary points A and B, with arbitrary radii R_A and R_B respectively, they are outside each other if and only if |AB|>|R_A+R_B|. 

Theorem 15. For any two circles which are centered at arbitrary points A and B, with arbitrary radii R_A and R_B respectively, they are outside each other except sharing one point on line AB if and only if |AB|=|R_A+R_B|. 

Theorem 16. For any two circles which are centered at arbitrary points A and B, with arbitrary radii R_A>R_B respectively, circle A is outside circle B if and only if |AB|<(R_A-R_B). 

Theorem 17. For any two circles which are centered at arbitrary points A and B, with arbitrary radii R_A>R_B respectively, circle A is outside circle B except sharing one point on line AB if and only if |AB|=(R_A-R_B). 

Theorem 14, Theorem 15, Theorem 16 and Theorem 17 can be concluded from Axiom 4.  For example, for Theorem 17, any point C on circle B satisfies |AC|<|AB|+R_B=R_A according to Theorem 13.  The only exception is where line AB is extended to meet circle B at point D, |AD|=|AB|+R_B=R_A, so that point D is on both circle A and circle B. 

Thus Theorem 17 is proven using deductive reasoning [41].  On the other hand, it is not possible to conclude Axiom 4 from Theorem 14, Theorem 15, Theorem 16 and Theorem 17, even though Axiom 4 seems to be only a case of relations between two circles together with the theorems.  It shows that in mathematics, logic uncovers hidden truth in observation.

6.2 Continuity

Figure 3: A straight line a passes point B inside a circle centered at A must intersect the circle at two points.

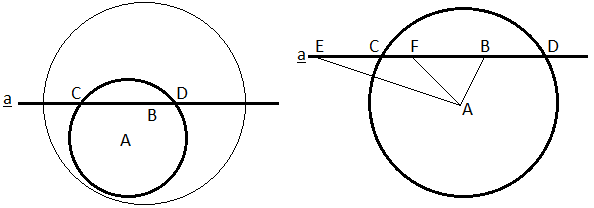
Although visually a circle is continuous by itself, continuity can only be proven mathematically as an intersecting property between two geometric objects.  Axiom 4 implied that a circle is continuous to another circle: if the condition is met, two circles will always intersect each other at one or two points.  Theorem 12 states that a circle is continuous to any straight line passing its center.  We will extend Theorem 12 by proving that a circle is continuous to any straight line passing any point inside the circle.

In Figure 3, a straight line a passes point B inside a circle centered at A.  According to Theorem 16, we can construct another circle centered at point B which is outside circle A, as shown in the left diagram of Figure 3.  According to Theorem 11, we can always find two points in either direction on line a which are outside circle B, thus also outside circle A, such as point E in the right diagram of Figure 3.  We now have point B inside circle A and point E outside circle A.  Let point F be the mid-point between the inside point B and the outside point E:

• If F is inside the circle A, points F and E become the new inside and the outside points.
• If F is outside the circle A, points B and F become the new inside and the outside points.

The above process keeps on dividing the original line EB into equal halves, with the length of the remaining line segments to fit into a series [42] of 1/2, 1/4, 1/8, 1/16, etc. of |EB|, which converges [42] to 0.  The process ends either by selecting point C on the circle as a new mid-point, or by converging to point C.  The same process can be carried out on the other side of the straight line a:

Theorem 18. If a straight line passes any point inside a circle, it must intersect the circle at two points: 1) the two points are on the circle, 2) the straight line segments between the two points are inside the circle, and 3) all the other points of the straight line are outside the circle.

The above process may need infinitive step to finish.  Because our goal is to prove the existence of intersecting point between the straight line and the circle, we can use the above process which is not practical.  In fact, we know that the mid-point for any line segment exists according to the requirement of distance, but we do not know how to find it yet. 

Theorem 18 is the extension of Theorem 12.

6.3 Tangent

For any straight line a and any point A which is not on a, the tangent point B has the shortest distance to the point A among all points on the straight line, and |AB| is called the distance between line a and any point A.  A trial case is that the point is on the straight line, in which the tangent point between the point and the straight line is the point itself, and the distance between the point and the straight line is 0.  Obviously, if a circle intersects a straight line at one point only, the point must be the tangent point between the straight line and the center of the circle.  We can use this relation to judge the intersection relation between a straight line and a circle:

Theorem 19. The necessary and sufficient condition for a straight line and a circle to intersect at two points is that the radius of the circle is more than the distance between the center of the circle and the straight line.

Theorem 20. The necessary and sufficient condition for a straight line and a circle to intersect at one point only is that the radius of the circle equals to the distance between the center of the circle and the straight line.

Theorem 21. The necessary and sufficient condition for a straight line and a circle to intersect at no points is that the radius of the circle is less than the distance between the center of the circle and the straight line.

6.4 Angle

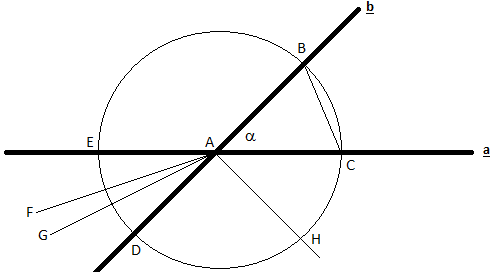
Figure 4: Angles formed by two intersecting straight lines

When two straight lines intersect each other according to Theorem 4, they form four rays, with each pair of rays forming an angle between them, as shown in Figure 4:

• The common starting point for the rays is called the vertex while the two rays are the two arms of the angle.  An angle can be referred to by its vertex between a point on each ray, such as \BAC or \CAB.  .
• \BAC and \BAE add to a straight line: they are supplementary angles.  \BAC and \CAD are also supplementary angles.
• Each respective arms of \BAC and \DAE form a straight line: they are opposite angles. 

In Figure 4, we can draw a circle centered at A with a predefined distance called the unit distance |u| as its radius, which intersects rays AB and AC at points B and C, respectively, according to Theorem 12.  The traditional measurement of angle \BAC uses the arc length between BC, but using such measurement of angle \BAC to calculate the arc length between BC [39], which easily leads to circular definitions [40].  In practice, defining or measuring the length of an arc is much more difficult than measuring a distance.  Thus, we define the angle distance ratio <\BAC> to measure \BAC in Figure 4 as <\BAC>º|BC|/|u|/2.  The angle distance ratio reveals the angular relation between any two rays which shares the same starting point.  We can construct an angle by known one of its arm and the angle distance ratio:

1. Draw a circle centered at point A with |u| as the radius, which interests ray AC at point C according to Theorem 12;
2. Draw a circle centered at point C with |BC|=2<\BAC>|u| as the radius, which interests the circle A at points B and H on two sides of line AC according to Axiom 4; 
3. Select point B by selecting on which side of ray AC to construct the angle;
4. Draw ray AB, to finish \BAC.

If two angles from vertex A and from the same side of ray AC have the same distance ratio, the circle centered at point C with |BC| as its radius will intersects the circle centered at point A with |u| as its radius at two points on each side of line AC, which violates Axiom 4.  Thus, there is one-to-one relation between <\BAC> and \BAC.  Two angles are said to be equal if they have an equal angle distance ratio. 

Theorem 22. Given a ray, a side selection related to the ray, and an angle distance ratio, one and only one angle can be constructed.

In Figure 4, visually an angle seems equal to its opposite angle but we cannot prove it.  In fact, we can cut out angle \FAG and stitch the space back along ray AF and AG, so that \BAC and \DAE are no longer equal.  In another word, \BAC and \DAE seem equal visually because of the underlying space homogeneity in Euclidean geometry.  Thus, rigid proof is very important in mathematics.

7. Space Homogeneity

7.1 Repeated

By observation, after a geometric object is moved and rotated on a flat plane, its properties which are not associated with position and orientation should not be changed.  The ability to translate [43] or rotate [44] a constructible object is embedded in how we construct it in most cases.  If a constructible object can be constructed by a first rule that contains 1) either a point (which is called a starting point), 2) or a ray (which is called a starting ray with its starting point), while all other rules only relate to each other including the first rule, then the constructible object is called a repeatable object.  The rules after the first rule are called the following rules.  The position of a repeated object is determined by its starting point, while its orientation is determined by its starting ray.  The properties of a repeatable object which are not related to the positions of starting point and the starting ray are called intrinsic properties, which is determined by the relation between its rules.  We use intrinsic properties to judge that the space is homogeneous:

According to Axiom 5, a point or a ray is the simplest repeatable object.  From how an angle is constructed in Theorem 22, we can see that an angle with a fixed angle distance ratio is a repeatable object.  We can select any point on a starting ray and extend the starting ray through the starting point and form a new ray.  The new ray and the starting ray form a straight angle with the angle distance ratio to be 1.  In Figure 4, angle \BAC and \DAE have the same starting point A but different starting rays.  After a rotation of a straight angle, ray AC becomes ray AE, while ray AB becomes ray AD, or angles \BAC and \DAE become the same geometric object by a rotation of a straight angle.  According to Axiom 5:

Theorem 23.  An angle equals to its opposite angle.

Two repeatable objects are repeated of each other if they have the same following rules.  For repeated objects, Axiom 5 can be simplified as:

Theorem 24.  All repeated objects have same intrinsic properties.

7.2 Triangle

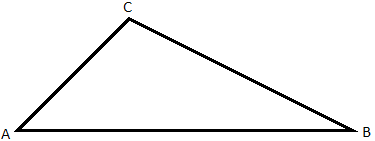
Figure 5  A triangle

For any three points which are not all on the same straight line, the geometric object which is formed by connecting these three points pair-wise using straight line segments is a triangle [45].  Each of these points is called a vertex, while each of these line segments is called a side.  The distance between any two vertexes is called the length for the side.  A triangle is usually referred by its three vertexes, such as triangle ABC in Figure 5.  Each vertex has one opposite side and two adjacent sides, with the two adjacent sides forming an angle at the vertex.  For example, side BC is the opposite side for vertex A, while the two adjacent sides AB and AC form the angle \BAC. 

Triangles and circles are the two basic shapes in Euclidian geometry, and they determine all the basic properties of Euclidian geometry.

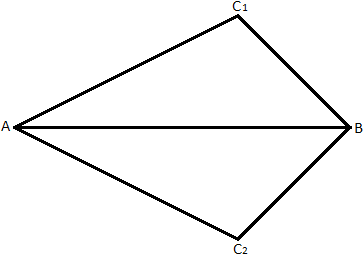
7.3 Reflected

In Figure 1, two triangles ABC and ABD seem mirror images of each other.  However, they are not repeated of each other, different in chirality [46].  The different choice for carrying out the following rules on which side of the starting ray is called reflection.  Unlike Theorem 24, which has been extended as a much broader axiom in science, Nature actually can distinguish and favor one chirality over another, such as DNA in nature always twisting right-handed [47].  But limited to our study, we could not favor one chirality over another, such as in Figure 1, so that we have to have an axiom to capture this reflected homogeneity:

Two repeatable objects are reflected of each other along the starting ray if they only differ in on which side of the starting ray the following rules are carried out.  For reflected objects, Axiom 6 can be simplified as:

Theorem 25. Any two reflected objects have same intrinsic properties except those properties which are reflection specific.

7.4 Congruent

The combination of repeated and reflected is called congruent [48].  According to Axiom 5 and Theorem 25：

Theorem 26.  Two congruent objects have same intrinsic properties except those properties which are reflection specific.

Both angle distance ratio and side length are intrinsic properties which are not reflection specific, while the sequence of count vertex for a triangle are reflection specific, as either clockwise or anticlockwise.  Using angle distance ratio and side length, there are many ways to construct congruent triangles.

If we want to construct a triangle from the length of three sides |AB|, |AC|, and |BC|:

1. Start on any side and any vertex, such as ray AB as in Figure 1;
2. Construct side AB using |AB|, by drawing a circle centered at A with |AB| as radius, to intersect ray AB at point B;
3. Draw two circles centered at point A and B, with radius R_A=|AC| and R_B=|BC|, respectively;
4. If circles A and B intersect at two points C and D according to Axiom 4, triangles ABC and ABD are reflected of each other.  Otherwise, such triangles are not possible.

Theorem 27. If all the corresponding sides of two triangles are equal in length, respectively, the two triangles are congruent.

Figure 6  Construct a triangle with a known angle and the length for two adjacent sides.

If the angle at a vertex A has known angle distance ratio <BAC>, and the length of the two adjacent sides |AB| and |AC| is known, as shown in Figure 6, we can:

1. Start from any adjacent side whose length is known, such as ray AB in Figure 6;
2. Construct side AB using |AB|;
3. Construct the angle on either side of the starting ray, as \BAC₁ and \BAC₂ using Theorem 22.
4. Construct the other adjacent side as AC₁ and AC₂ using |AC|;
5. Connect end point B to C₁ or C₂, to result in two triangles ABC₁ and ABC₂, which are reflected of each other.

Theorem 28.  If two triangles have one angle equal, and the length of the two adjacent sides of the angle also equal, respectively, then the two triangles are congruent.

Figure 7  Construct a triangle with a known angle, and the length for the opposite side and one adjacent side.

If the angle at a vertex A has known angle distance ratio <BAC>, and the length of one adjacent side |AB| and the length of the opposite side |BC| is known, as shown in Figure 7, we can:

1. Start from A to construct ray AB;
2. Construct side AB using |AB|;
3. Construct the angle on either side of the starting ray, as \BAC₁ and \BAC₂;
4. Draw a circle centered at point B, with |BC| as the radius;
5. When |BC|>|AB|, the circle will intersect the adjacent side at one point only, such as C₁ in the right diagram for Figure 7, and two reflected triangles ABC₁ and ABC₂ are constructed.  Otherwise, such triangles are either not possible, or not uniquely constructible as in the left diagram for Figure 7.

Theorem 29.  If two triangles have one angle equal, the length of one adjacent side and the opposite side of the angle also equal, respectively, the length of the opposite side is more than the known length of the adjacent sides, then the two triangles are congruent.

8. Measure the flat plane

Before we can tell whether a 2-dimensional space is flat or not, we need to measure the plane.  We will achieve this goal by exploring the visual symmetry of the flat plane using straight lines.

8.1 Perpendicular

Let’s first find if two straight line can cross each other in a special case.  If an angle equals to that of its supplementary angle, according to Theorem 23, the four angles generated by the intersecting of the two straight lines a and b are all equal, each of which is a right angle, and the two line a and b are perpendicular to each other, or a#b.  

Two perpendicular straight lines are not interesting by themselves.  We need to look at them in the context of related triangles, as shown in Figure 8:

Theorem 30. For two straight lines a and b which intersect each other at point B, with A and E being any two points on b, C and D being any two points on a, if any two of the following four statements stand, the remaining two statements also stand: 1) a#b; 2) |BC|=|BD|; 3) |AC|=|AD|; 4) |EC|=|ED|.

Figure 8: the associated triangles for straight lines a#b

By observation, the diagram is reflected along line b so we can prove Theorem 30 accordingly:

• a#b and |BC|=|BD|: According to Theorem 28, triangles ABC and ABD are congruent so that |AC|=|AD|, while triangles EBC and EBD are congruent so that |EC|=|ED|.
• |BC|=|BD| and |AC|=|AD|: According to Theorem 27, triangles ABC and ABD are congruent so that a#b.  According to Theorem 28, triangles EBC and EBD are congruent so that |EC|=|ED|.
• |AC|=|AD| and |EC|=|ED|: According to Theorem 27, triangles AEC and AED are congruent so that \BAC=\BAD.  According to Theorem 28, triangles ABC and ABD are congruent so that |BC|=|BD| and a#b.
• a#b and |AC|=|AD|: If we make a circle centered at A with |AC| as its radius, the circle intersects line a at points C and D.  According to Theorem 18, B is inside the circle, so that |AB|<|AC|.  According to Theorem 29, triangles ABC and ABD are congruent so that |BC|=|BD|.  According to Theorem 28, triangles EBC and EBD are congruent so that |EC|=|ED|.

In Figure 8, because \BAC equals \BAD, ray AB bisects \CAD.

Because B is the mid-point of line CD, B is unique according to Theorem 8.  Thus line b is also unique passing point A and perpendicular to line a.  Assume that we draw a circle centered at A with |AB| as radius, and this circle intersects line a at another point X.  According to Theorem 30, we can draw another straight line which passes the mid-point of line BX and which is perpendicular to line a.  Such a straight line violates the uniqueness of line b, so that B is also the tangent point between the straight line a and the point A according to 0. 

Theorem 31. For a straight line and a point, there is one and only one straight line which passes the point and which is perpendicular to the straight line, at the tangent point between the point and the straight line.

Using Theorem 30, we can:

• For a straight line and a point, draw another straight line which passes the point and which is perpendicular to the straight line at their tangent point.
• For a straight line segment, draw a straight line which is perpendicular to the line segment, and intersects the line segment at the mid-point of the line segment.
• Bisect an angle into two equal angles.  For example, in Figure 8, line AB bisects \CAD.

8.2 Right triangle

A triangle is a right triangle if it has a right angle. 

Figure 9  Construct a right triangle with a known other angle and the length for the side opposite to the right angle.

We can construct a right triangle by knowing the distance ratio of one other angle \BAC in addition to the right angle \ABC and the length of any side, such as |AC| of the side opposite to the right angle at vertex C, as shown in Figure 9:

1. Start on ray AB;
2. Construct angle \BAC on each side of ray AB according to Theorem 22.
3. Construct side AC₁ and AC₂ using |AC| on the other ray of angle A, respectively;
4. Construct lines C₁C₂#AB, with C₁C₂ intersects ray AB at point B, according to Theorem 30.

Theorem 32. Two right triangles are congruent if any other angles in addition to the right angle are equal, and the sides opposite to the right angles have equal length.

8.3 Parallel

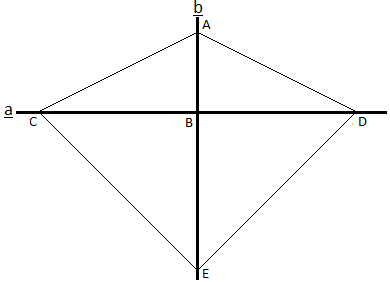
What happens if more than one straight lines perpendicular to the same straight line? As indicated in Figure 10, they are parallel to each other.  Figure 10 also shows that the perpendicular relation can be between two sets of parallel lines. We will reveal such a relation step by step, using straight line a, b, c, d and their intersecting points A, B, C, D in Figure 10.

Figure 10:  Two sets of parallel lines perpendicular to each other.

If a#b and a#c, lines b and c cannot intersect each other; otherwise Theorem 31 is violated.  Two straight lines are parallel to each other if they do not intersect each other, such as b||c.   

Theorem 33. If two straight lines are both perpendicular to a common straight line, then these two straight lines are parallel to each other.

For an arbitrary point A and an arbitrary straight line c, we can first use Theorem 31 to draw a straight line a#c passing A, then draw another line d#a passing A.  According to Theorem 33, d||c.  According to Theorem 31, d is unique. 

Theorem 34. For a straight line and a point, there can be one and only one straight line that is parallel to the straight line and passes the point.

If a||b and c#a, from a point on b, we can draw d#c.  According to Theorem 33, d||a, which violates Theorem 34 unless d and b are the same straight line.  Thus:

Theorem 35. For two parallel straight lines, if one of them is perpendicular to a third straight line, then the other straight line also is perpendicular to the third straight line.

If a||b and b||e, from a point on b, according to Theorem 35, we can draw a straight line x perpendicular to both a and b, and another straight line y perpendicular to both b and c.  According to Theorem 31, x and y has to be the same straight line.  According to Theorem 33, a||e.

Theorem 36.  If a||b and b||c, then a||c.

Theorem 33, Theorem 35 and Theorem 36 show that perpendicular relationship can also be between two sets of parallel straight lines.  Theorem 31 and Theorem 34 show the uniqueness of either perpendicular or parallel relation between a point and a straight line.

8.4 Parallel Lines on a Flat Plane

When two straight lines are parallel to each other, they are always in the vicinity of each other, which provides good case to measure a plane.  In Figure 11, the two straight lines a||b.  Another straight line c seems to intersect both of them at equal angles.  We will explore this property to measure the plane.

Figure 11 Lines a||b, while line c intersects both of them

In Figure 11, c intersects a at point A with angle \CAD.  c must intersect line b at some point B at angle \CBE; otherwise Theorem 34 is violated at point A.  We can find the mid-point C between A and B.  From C, we can draw a line d#a and d#b according to Theorem 35, which intersects lines a and b at point D and E, respectively.  According to Theorem 23 and Theorem 32, triangles CAD and CBE are congruent.  Thus, angles \CAD and \CBE are equal.  Because \CAD and \CBE are both between a||b, they are called inner angles for c passing through a||b.

Theorem 37.  If a||b, and c intersect a, then c also intersects b with an equal inner angle.

Theorem 37 can be used to judge whether the 2-dimensional space is flat or not.  On a sphere, we can use a latitude line to produce a set of longitude lines, and draw another great circle other than the latitude line to intersect the set of longitude lines.  At the equator, Theorem 37 is correct, but if we travel either north or south, Theorem 37 is broken.  The more we are away from the equator, the more obviously Theorem 37 is broken.

Figure 12 The sum of three angles in a triangle

In Figure 12, for any triangle ABC, we can always make a straight line passing C and parallel to line AB.  According to Theorem 37, \ACD equals \CAB, \BCE equals \ABC, while the three angles \ACD, \BCE and \ACB of the triangle ABC add up to a straight line. 

Theorem 38.  The three angles of any triangle add up to a straight line.

Theorem 38 can be used to test whether the plane is flat or not by testing whether the inner angles for \ACD and \BCE are equal, respectively, as in Figure 12.  The advantage of using Theorem 38 instead of Theorem 37 for such test is that the result does not depend on any location, but only on the triangle itself.  Such independence is very valuable when the 2-dimensional space deviates from a flat plane at different locations, such as due to general relativity [18].

8.5 Grid and area

In Figure 10, straight line sets a||b # c||d, according to Theorem 35.  According to Theorem 37, \ACB equals \DAC.  According to Theorem 32, triangles ABC and ABD are congruent, so that |AB|=|CD| and |AD|=|BC|.  All the perpendicular straight lines to two parallel straight lines have same distance between the two parallel straight lines, which is called the distance between the two parallel straight lines. 

The repeatable object which is formed by a pair of parallel straight lines perpendicular to each other is call a rectangle, such as rectangle ACBD in Figure 10.  If both pairs have the same distance between the lines, the rectangle becomes a square.

Figure 13:  Use grid to measure a flat space.

To measure a flat plane, we can make a grid using two sets of parallel straight lines with each straight line having equal distance to the next two straight lines in the set, and with each set perpendicular to the other, as shown in Figure 13.  The grid divides a flat plane into congruent squares.  The area is the count of the grid squares in principle.  As shown in Figure 13, the area for a rectangle is thus defined as a*b, in which a and b are the length of the two sides to the rectangle, respectively.  The area has to be a definition because both a and b can be irrational, so that counting is not possible.  In this case, definition also contains generalization.  According to Figure 10, the area of a right triangle is a*b/2, in which a and b are the length of the two adjacent sides to the right angle, respectively.  Thus, area as a measurement, is derived from distance. 

Figure 14:  Right triangle and the proof of Pythagorean Theorem.

Let the length of the side opposite to the right angle in a right triangle be c.  We can arrange four congruent right triangles within a rectangle as in Figure 14 according to Theorem 32, to result in the relationship of a²+b²=c².

Theorem 39.  For any right triangle with c as the length of the side opposite to the right angle, a and b as the lengths of the other two sides, respectively, then a²/c² + b²/c² = 1.

Theorem 39 can also be used to test whether the plane is flat or not.  The advantage of using Theorem 39 instead of Theorem 38 for such a test is that minimal distance measurement is required.  On the other hand, each measurement of the angle distance ratio needs to reproduce unit distance on the two rays of the angle before measuring the distance for the distance ratio calculation, as shown in Figure 4.  A valid question is whether a distance can be reproduced to a different location in a space, such as in a bent space, where a straight line can bend and a distance can shrink [18].  Thus, Theorem 39 is more practical than Theorem 38 in measuring whether a 2-dimensional space is flat or not. 

8.6 Error reduction

The distance relations in Theorem 39 are in normalized form, a²/c²+b²/c²=1, rather than the usual a²+b²=c² form, so that the result no longer depends on the unit in which a, b and c are measured.

Figure 15:  Error reduction in experimental proof of Pythagorean Theorem.

Besides measurement error [49] of distance, the test for a²/c²+b²/c²=1 on a right triangle depends on our ability to make a precise right angle.  In Figure 15, triangles ECB and ECD deviate from perfect right triangles ACB and ACD, respectively, so that |EB|<|AB| while |ED|>|AD|.  If the deviation from the right angle is small, we could approximate the error dc on c as |EC|»|AC|-dc  and |ED|»|AD|+dc.  To cope with such error, we can:

• Make multiple right angles, and average the measurement results, to let random errors [49] cancel out each other.  For example, if  for each measurement is purely due to random error, the error for the averaged result reduces as  [49], in which N is the number of measurements.
• Improve measurement design by creating triangles EBC and EBD together, and average |EC| and |ED| directly to get .  In this way, the measurement errors including the systematic errors [49] due to the right angle measurement largely cancel out each other.

The study of measurement error [49] is also an important branch of mathematics.  Mathematics is not only beautiful, but also useful.

9. Discussion and Conclusion

Theorem 39 is called the Pythagorean Theorem [36], which is a paramount achievement of Euclidean geometry for a flat plane.  It is the base of establishing a Cartesian coordinate system [50] on a flat plane, which is the base for analytic geometry [51] that enables the study of more complex shapes, and more general geometries [52]. 

Perhaps it is unique for a mathematic thesis to emphasize direct observation as the very first step in the four-step approach in this paper.  Indeed, the author of this paper was trained as an experimental physicist rather than as a mathematician.  For example, this paper only distinguishes between 1) the flat plane as a special case for Euclidean geometry [1], and 2) the sphere as a special case for elliptic geometry [52]; but it leaves out any case for hyperbolic geometry [54], because there is no observable homogenous 2-dimensional space as a special case for hyperbolic geometry.  A mathematician by training may have different approach, such as excluding such possibility mathematically [55].  As a thesis for high school students, the approach in this paper seems more appropriate, while it is still mathematically strictly even without mentioning any hyperbolic geometry.

Using 6 axioms as the 6 unique properties of the flat plane, we have completely described the flat plane and a few repeatable objects on the flat plane, even though these axioms seem too simple to describe such an organic system at first—this process shows the magic of mathematics.  One thing peculiar is that we have not defined what a flat plane is, yet as a result we have ways to fully describe it and test it.  In fact, we are not able to make such a definition, because it is among our basic assumptions, being implied in the 6 axioms.

By using the great circle instead of a straight line between any two points, the adopted 6 axioms can completely describe a sphere.  By adopting Axiom 4 to limit the space to be 3-dimensional, and by adding a new axiom that any three different points determine a flat plane, the axioms can completely describe a Euclidean 3-dimensional space.  Euclidean geometry can be extended in several ways.  The different ways to violate Theorem 34 lead to different non-Euclidean geometries [56].  Axiom 3 is the foundation for metric system [57].  The geometric system without Axiom 3 is called affine geometry [58].  Thus, such concise yet strict and complete description of a flat plane is not by chance, but by the power of mathematics.

Compared to the axioms in the traditional Euclidean geometry, we only use 6 axioms, with the context for each axiom very clear: 

1. Axiom 1 requires that the space to be stable;
2. Axiom 2 states a unique property of straight lines in any Euclidean space;
3. Axiom 3 states that any Euclidean space can be measured by distance;
4. Axiom 4 limits the Euclidean space to be 2-dimensional;
5. Axiom 5 states the 2-dimensional Euclidean space to be repeated equivalence;
6. Axiom 6 states the 2-dimensional Euclidean space to be reflected equivalence.

So we have gained something valuable by reinventing the wheel, even though our conclusion is identical to that of traditional Euclidean geometry.  We have achieved this understanding by asking questions logically in steps, following the four steps of studying science in general.  Perhaps it would not be a bad idea to try to reinvent the wheel first when studying a new subject, before we actually read existing results:

• If we made a mistake or a worse approach, we can learn something.
• If we were correct or even better, we can invent something.

10. Acknowledgement

The author of this paper thanks 1) the president of Institute of Creative Problem Solving, Mr. Arthur Knish, who gave me a chance to write and present my idea to a selected elite math class of high school students in December, 2016, 2) the reviewers for Mathematics Teachers’ Journal, who encouraged me to continue working on the idea while pointing out defects in the original draft of the paper, and 3) my daughter Alice, whose good questions start this paper.

11. Reference

[1].              Euclidean geometry, Wikipedia: https://en.wikipedia.org/wiki/Euclidean_geometry.

[2].              Hilbert’s axioms, Wikipedia: https://en.wikipedia.org/wiki/Hilbert%27s_axioms.

[3].              Mathematical logic, Wikipedia: https://en.wikipedia.org/wiki/Mathematical_logic.

[4].              Formal system, Wikipedia: https://en.wikipedia.org/wiki/Formal_system.

[5].              Fractal dimension, Wikipedia: https://en.wikipedia.org/wiki/Fractal_dimension.

[6].              Observation, Wikipedia: https://en.wikipedia.org/wiki/Observation.

[7].              Generalization, Wikipedia: https://en.wikipedia.org/wiki/Generalization.

[8].              Axiom, Wikipedia: https://en.wikipedia.org/wiki/Axiom.

[9].              Precising definition, Wikipedia: https://en.wikipedia.org/wiki/Precising_definition.

[10].          Theorem, Wikipedia: https://en.wikipedia.org/wiki/Theorem.

[11].          Consistency, Wikipedia: https://en.wikipedia.org/wiki/Consistency.

[12].          Tacit assumption, Wikipedia: https://en.wikipedia.org/wiki/Tacit_assumption.  [5]

[13].          Measurement, Wikipedia: https://en.wikipedia.org/wiki/Measurement.

[14].          Test method, Wikipedia: https://en.wikipedia.org/wiki/Test_method.

[15].          High School Geometry, Common Core State Standards Initiative: https://www.corestandards.org/Math/Content/HSG/introduction/.

[16].          List of mathematics competitions, Wikipedia: https://en.wikipedia.org/wiki/List_of_mathematics_competitions.

[17].          Advanced Placement, Wikipedia: https://en.wikipedia.org/wiki/Advanced_Placement.

[18].          General relativity, Wikipedia: https://en.wikipedia.org/wiki/General_relativity.

[19].          String theory, Wikipedia: https://en.wikipedia.org/wiki/String_theory.

[20].          Thought experiment, Wikipedia: https://en.wikipedia.org/wiki/Thought_experiment.

[21].          Set, Wikipedia: https://en.wikipedia.org/wiki/Set_(mathematics).

[22].          Idealization, Wikipedia: https://en.wikipedia.org/wiki/Idealization.

[23].          Sphere, Wikipedia: https://en.wikipedia.org/wiki/Sphere.

[24].          Ruler, Wikipedia: https://en.wikipedia.org/wiki/Ruler.

[25].          Proof by contradiction, Wikipedia: https://en.wikipedia.org/wiki/Proof_by_contradiction.

[26].          Metric system, Wikipedia: https://en.wikipedia.org/wiki/Metric_system.

[27].          Light-year, Wikipedia: https://en.wikipedia.org/wiki/Light-year.

[28].          Linear scale, Wikipedia: https://en.wikipedia.org/wiki/Linear_scale.

[29].          Logarithmic scale, Wikipedia: https://en.wikipedia.org/wiki/Logarithmic_scale.

[30].          Compass, Wikipedia: https://en.wikipedia.org/wiki/Compass_(drawing_tool).

[31].          Abstraction (mathematics) , Wikipedia: https://en.wikipedia.org/wiki/Abstraction_(mathematics).

[32].          Real number, Wikipedia: https://en.wikipedia.org/wiki/Real_number.

[33].          Necessity and sufficiency, Wikipedia: https://en.wikipedia.org/wiki/Necessity_and_sufficiency.

[34].          Integer, Wikipedia: https://en.wikipedia.org/wiki/Integer.

[35].          Rational number, Wikipedia: https://en.wikipedia.org/wiki/Rational_number.

[36].          Pythagorean Theorem, Wikipedia: https://en.wikipedia.org/wiki/Pythagorean_theorem.

[37].          Irrational number, Wikipedia: https://en.wikipedia.org/wiki/Irrational_number.

[38].          Mobius plane, Wikipedia:https://en.wikipedia.org/wiki/Mobius_strip.

[39].          Angle, Wikipedia: https://en.wikipedia.org/wiki/Angle.

[40].          Circular definition, Wikipedia: https://en.wikipedia.org/wiki/Circular_definition.

[41].          Deductive reasoning, Wikipedia: https://en.wikipedia.org/wiki/Deductive_reasoning.

[42].          Series (mathematics), Wikipedia: https://en.wikipedia.org/wiki/Series_(mathematics).

[43].          Translation, Wikipedia: https://en.wikipedia.org/wiki/Translation_(geometry).

[44].          Rotation, Wikipedia: https://en.wikipedia.org/wiki/Rotation.

[45].          Triangle, Wikipedia: https://en.wikipedia.org/wiki/Triangle.

[46].          Chirality, Wikipedia: https://en.wikipedia.org/wiki/Chirality_(mathematics).

[47].          DNA, Wikipedia: https://en.wikipedia.org/wiki/DNA.

[48].          Congruence (geometry), Wikipedia: https://en.wikipedia.org/wiki/Congruence_(geometry).

[49].          Observational error, Wikipedia:  https://en.wikipedia.org/wiki/Observational_error.

[50].          Cartesian coordinate system, Wikipedia: https://en.wikipedia.org/wiki/Cartesian_coordinate_system.

[51].          Analytic geometry, Wikipedia: https://en.wikipedia.org/wiki/Analytic_geometry.

[52].          Riemannian geometry, Wikipedia: https://en.wikipedia.org/wiki/Riemannian_geometry.

[53].          Elliptic geometry, Wikipedia: https://en.wikipedia.org/wiki/Elliptic_geometry. 

[54].          Hyperbolic geometry, Wikipedia: https://en.wikipedia.org/wiki/Hyperbolic_geometry.

[55].          Hilbert’s theorem (differential geometry), Wikipedia: https://en.wikipedia.org/wiki/Hilbert%27s_theorem_(differential_geometry).

[56].          Non-Euclidean geometry, Wikipedia: https://en.wikipedia.org/wiki/Non-Euclidean_geometry.

[57].          Metric system, Wikipedia:https://en.wikipedia.org/wiki/Metric_space.

[58].          Affine geometry, Wikipedia: https://en.wikipedia.org/wiki/Affine_geometry.

[59].